题目内容
6．
一个几何体是由一些大小相同的小立方块摆成的，其主视图和俯视图如图所示，则组成这个几何体的小立方块最少有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
分析 从俯视图中可以看出最底层小正方体的个数及形状，从主视图可以看出每一层小正方体的层数和个数，从而算出总的个数．
解答 解：由题中所给出的主视图知物体共两列，且左侧一列高两层，右侧一列最高一层；
由俯视图可知左侧两行，右侧一行，于是，可确定左侧只有一个小正方体，而右侧可能是一行单层一行两层，出可能两行都是两层．
所以图中的小正方体最少4块，最多5块．
故选：B．
点评 本题主要考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．
练习册系列答案
相关题目
16．点P（2，-6）所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
17．
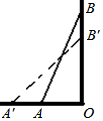如图，梯子AB靠在墙上，梯子底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，那么BB′（ ）
如图，梯子AB靠在墙上，梯子底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，那么BB′（ ）| A． | 小于1 m | B． | 大于1 m | C． | 等于1 m | D． | 小于或等于1 m |
14．下列各数中是无理数的是（ ）
| A． | 3.14 | B． | $\sqrt{16}$ | C． | $\frac{2}{3}$ | D． | $\sqrt{6}$ |
1．
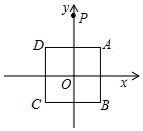如图，在平面直角坐标系中，正方形ABCD的顶点A（1，1），B（1，-1），C（-1，-1），D（-1，1），y轴上有一点P（0，2），作点P关于点A的对称点P1，作点P1关于点B的对称点P2，作点P2关于点C的对称点P3，作点P3关于点D的对称点P4，作点P4关于点A的对称点P5，作点P5关于点B的对称点P6，…，按此规律操作下去，则点P2017的坐标为（ ）
如图，在平面直角坐标系中，正方形ABCD的顶点A（1，1），B（1，-1），C（-1，-1），D（-1，1），y轴上有一点P（0，2），作点P关于点A的对称点P1，作点P1关于点B的对称点P2，作点P2关于点C的对称点P3，作点P3关于点D的对称点P4，作点P4关于点A的对称点P5，作点P5关于点B的对称点P6，…，按此规律操作下去，则点P2017的坐标为（ ）| A． | （2，0） | B． | （0，2） | C． | （0，-2） | D． | （-2，0） |
11．
如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD=30°，则∠BAD为（ ）
如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD=30°，则∠BAD为（ ）| A． | 30° | B． | 50° | C． | 60° | D． | 70° |
18．已知一列数：1，-2，3，-4，5，-6，7，…将这列数排成下列形式：
第1行 1
第2行-2 3
第3行-4 5-6
第4行 7-8 9-10
第5行 11-12 13-14 15
…
按照上述规律排下去，那么第100行从左边数第5个数是（ ）
第1行 1
第2行-2 3
第3行-4 5-6
第4行 7-8 9-10
第5行 11-12 13-14 15
…
按照上述规律排下去，那么第100行从左边数第5个数是（ ）
| A． | -4955 | B． | 4955 | C． | -4950 | D． | 4950 |
15．
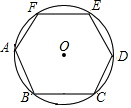正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是（ ）
正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
16．
如图，在菱形ABCD中，对角线AC、BD相交于点O，点E、F分别是边AB、BC的中点，连接EF，若EF=3，BD=6$\sqrt{3}$，则菱形ABCD的面积为（ ）
如图，在菱形ABCD中，对角线AC、BD相交于点O，点E、F分别是边AB、BC的中点，连接EF，若EF=3，BD=6$\sqrt{3}$，则菱形ABCD的面积为（ ）| A． | 6$\sqrt{3}$ | B． | 9$\sqrt{3}$ | C． | 18$\sqrt{3}$ | D． | 36$\sqrt{3}$ |