题目内容
7.某社区计划对面积为1800m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队的2倍;当两队分别各完成400m2的绿化时,甲队比乙队少用4天.(1)求甲、乙两工程队每天能完成的绿化的面积;
(2)两队合作完成此项工程,若甲队参与施工n天,试用含n的代数式表示乙队施工的天数;
(3)若甲队每天施工费用是0.6万元,乙队每天为0.25万元,且要求两队施工的天数之和不超过26天,应如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低费用.
分析 (1)设乙工程队每天能完成绿化的面积是xm2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
(2)甲、乙工作总量是1800;
(3)求出w与n的函数解析式,根据n的取值范围以及一次函数的性质求解即可.
解答 解:(1)设乙工程队每天能完成绿化的面积是xm2,
根据题意得:$\frac{400}{x}$-$\frac{400}{2x}$=4,
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2;
(2)由(1)可知,甲队每天能完成绿化的面积为100m2,乙队每天能完成绿化的面积为50m2,
所以依题意得:100x+50y=1800,
化简得y与x的函数关系式为:y=-2x+36;
(3)由于甲、乙两队施工的总天数不超过26天,
所以,x+y≤26.
由(2)可得y=-2x+36,
代入可得x-2x+36≤26,
解得x≥10.
设施工总费用为w万元,则w=0.6x+0.25y=0.6x+0.25(36-2x)=0.1x+9.
因为0.1>0,由一次函数性质可知,w随x的增大而增大,
所以当x取最小值,即x=10天时,总费用w最低,且最小值为:0.1×10+9=10(万元),
此时y=-2×10+36=16(天).
故甲队施工10天,乙队施工16天,施工费用最低为10万元.
点评 本题考查了分式方程和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | 2a×3a=5a | B. | (-2a)3=-6a3 | C. | 6a÷2a=3a | D. | (-a3)2=a6 |
15.一次函数y=kx-k(k>0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
2.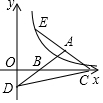 如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )
如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )
 如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )
如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
12.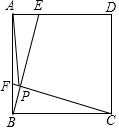 如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
 如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$-2 | D. | 2$\sqrt{5}$-2 |
16.点P(2,-6)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.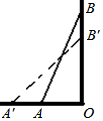 如图,梯子AB靠在墙上,梯子底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
如图,梯子AB靠在墙上,梯子底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
 如图,梯子AB靠在墙上,梯子底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )
如图,梯子AB靠在墙上,梯子底端A到墙根O的距离为2m,梯子的顶端B到地面的距离为7m,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3m,同时梯子的顶端B下降至B′,那么BB′( )| A. | 小于1 m | B. | 大于1 m | C. | 等于1 m | D. | 小于或等于1 m |
