题目内容
8.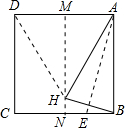 如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )
如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )①AE垂直平分HB;②∠HBN=15°;③DH=DC;④△ADH是一个等边三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由翻折的性质可知;点H与点B关于AE对称,故此AE⊥BH,④由翻折的性质AH=AB,MN垂直平分AD,于是得到DH=AH=AB=AD,故此△ADH为等边三角形,③由DH=AD可知DH=DC,②由△ADH为等边三角形可知∠HAB=30°,在△ABH中可求得∠ABH=75°,故此可求得∠HBN=15°.
解答 解:由翻折的性质可知:AE垂直平分HB,MN垂直平分AD.
故①正确.
∵MN垂直平分AD,
∴DH=AH.
由翻折的性质可知:AH=AB.
∴AH=AD=DH.
∴△ADH是一个等边三角形.
故④正确.
∵HD=AD,
∴HD=DC.
故③正确
∵△ADH是一个等边三角形,
∴∠DAH=60°.
∴∠HAB=30°.
∵AB=AH,
∴∠ABH=$\frac{1}{2}$×(180°-30°)=75°.
∴∠HBN=15°.
故②正确.
故选:D.
点评 本题主要考查的是翻折的性质、线段垂直平分线的性质、等边三角形的性质和判定、等腰三角形的性质,证得三角形ADH是一个等边三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列各式中互为相反数的算式是( )
①-(-3)②(-3)2 ③|-(-3)|④-|-32|
①-(-3)②(-3)2 ③|-(-3)|④-|-32|
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
20.多项式2xy-3xy2+25的次数及最高次项的系数分别是( )
| A. | 3,-3 | B. | 2,-3 | C. | 5,-3 | D. | 2,3 |
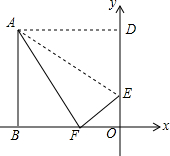 在平面直角坐标系中,长方形ODAB的边OB在x轴上,OD在y轴上,点O为原点,边OB=10,AB=8,将长方形沿AE翻折,使点D落在边OB上的点F处,则AE所在直线的表达式为y=-$\frac{1}{2}$x+3.
在平面直角坐标系中,长方形ODAB的边OB在x轴上,OD在y轴上,点O为原点,边OB=10,AB=8,将长方形沿AE翻折,使点D落在边OB上的点F处,则AE所在直线的表达式为y=-$\frac{1}{2}$x+3. 将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形.
将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形. 如图是由五个小正方体组成的立体图形,则从左面看到的平面图形是( )
如图是由五个小正方体组成的立体图形,则从左面看到的平面图形是( )



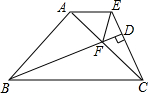 如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.
如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.