题目内容
2.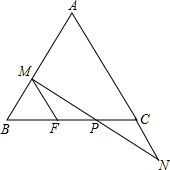 在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.
在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.(1)求证:△PMF≌△PNC;
(2)求证:BM=CN.
分析 (1)由平行线的性质得出∠MFP=∠NCP,由AAS证明△PMF≌△PNC即可;
(2)由全等三角形的性质得出FM=CN,由等腰三角形的性质和平行线的性质得出∠B=∠MFB,证出BM=FM,即可得出结论.
解答 (1)证明:∵MF∥AN,
∴∠MFP=∠NCP,
在△PMF和△PNC中,
$\left\{\begin{array}{l}{∠MFP=∠NCP}&{\;}\\{∠MPF=∠NPC}&{\;}\\{PM=PN}&{\;}\end{array}\right.$,
∴△PMF≌△PNC(AAS);
(2)证明:由(1)得:△PMF≌△PNC,
∴FM=CN,
∵AB=AC,
∴∠B=∠ACB,
∵MF∥AN,
∴∠MFB=∠ACB,
∴∠B=∠MFB,
∴BM=FM,
∴BM=CN.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
20.多项式2xy-3xy2+25的次数及最高次项的系数分别是( )
| A. | 3,-3 | B. | 2,-3 | C. | 5,-3 | D. | 2,3 |
12.在△ABC中,∠C=90°,BC=3,AB=5,则sinA的值是( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
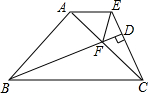 如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.
如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.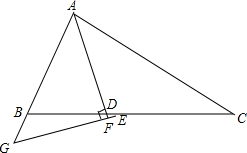 已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.
已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG. 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.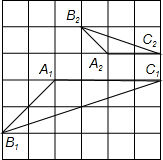 学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.