题目内容
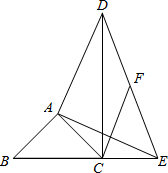 已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE.
已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE.(1)求证:△ABE≌△ACD;
(2)如果点F是DE的中点,求证:CF=DF.
考点:全等三角形的判定与性质,直角三角形斜边上的中线,等腰直角三角形
专题:证明题
分析:(1)根据DA⊥AE,得出∠DAE=90°,再根据∠BAC=90°,得出∠BAC+∠CAE=∠DAE+∠CAE,即可证出△ABE≌△ACD;
(2)根据△ABE≌△ACD,得出∠B=∠ACD,再根据∠B=∠ACB,∠B+∠ACB=90°,得出∠DCE=90°,最后根据点F是DE的中点,得出CF=DF.
(2)根据△ABE≌△ACD,得出∠B=∠ACD,再根据∠B=∠ACB,∠B+∠ACB=90°,得出∠DCE=90°,最后根据点F是DE的中点,得出CF=DF.
解答:(1)证明:∵DA⊥AE,
∴∠DAE=90°,
∵∠BAC=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
在△ABE和△ACD中,
∵
,
∴△ABE≌△ACD;
(2)证明:∵△ABE≌△ACD,
∴∠B=∠ACD,
∵∠B=∠ACB,∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,
∴∠DCE=90°,
∵点F是DE的中点,
∴CF=
DE=DF;
∴∠DAE=90°,
∵∠BAC=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
在△ABE和△ACD中,
∵
|
∴△ABE≌△ACD;
(2)证明:∵△ABE≌△ACD,
∴∠B=∠ACD,
∵∠B=∠ACB,∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,
∴∠DCE=90°,
∵点F是DE的中点,
∴CF=
| 1 |
| 2 |
点评:此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质,直角三角形的性质,解题的关键是证出∠BAE=∠CAD.

练习册系列答案
相关题目
任意选择一对有序整数(b,c),其中每一个整数的绝对值小于或等于5,每一对这样的有序整数被选择的可能性是相等的.方程x2+bx+c=0没有相异正实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
化简
+
的值为( )
4-
|
4+
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB是⊙O直径,AC是弦,OD⊥CB于点D,若OD=3,则AC=
如图,AB是⊙O直径,AC是弦,OD⊥CB于点D,若OD=3,则AC= 已知△ABC中,AB=AC,以AB为直径的⊙O1分别交AC、BC于两D、E点,过B点的切线交OE的延长线于点F,连FD、BD、OD,下列结论:①四边形ODCE是平行四边形;②E是△BFD的内心;③E是△FDO的外心;④∠C=∠BFD;其中正确的有( )个.
已知△ABC中,AB=AC,以AB为直径的⊙O1分别交AC、BC于两D、E点,过B点的切线交OE的延长线于点F,连FD、BD、OD,下列结论:①四边形ODCE是平行四边形;②E是△BFD的内心;③E是△FDO的外心;④∠C=∠BFD;其中正确的有( )个.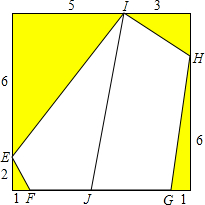 在正方形ABCD中,切去四个三角形得到一个五边形EFGHI(如图,其中所标的数表示各线段的长度),线段IJ将五边形EFGHI分成两个面积相等的部分,那么FJ的长度是
在正方形ABCD中,切去四个三角形得到一个五边形EFGHI(如图,其中所标的数表示各线段的长度),线段IJ将五边形EFGHI分成两个面积相等的部分,那么FJ的长度是