题目内容
7. 如图,已知菱形ABCD中,∠ABC=60°,AB=6,点E是AB的中点,F是边BC上的任意一点,将△BEF沿EF折叠,B点的对应点为B′,连接B'C,则B'C的最小值为3$\sqrt{3}$-3.
如图,已知菱形ABCD中,∠ABC=60°,AB=6,点E是AB的中点,F是边BC上的任意一点,将△BEF沿EF折叠,B点的对应点为B′,连接B'C,则B'C的最小值为3$\sqrt{3}$-3.
分析 连接CE,根据三角形的三边关系找出当点B′在CE上B'C最小,通过解直角三角形得出CE的长度,再由边与边之间的关系即可算出B'C的最小值.
解答 解:连接CE,如图所示.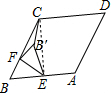
∵将△BEF沿EF折叠,B点的对应点为B′,
∴BE=B′E,
∴B'C≥CE-B′E(三角形任意两边之差小于第三边),当点B′在CE上取等号.
∵菱形ABCD中,∠ABC=60°,AB=6,点E是AB的中点,
∴∠BCE=30°,∠BEC=90°,
∴CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=3$\sqrt{3}$,
∴B′C≥CE-B′E=3$\sqrt{3}$-3.
故答案为:3$\sqrt{3}$-3.
点评 本题考查了翻折变换、菱形的性质、含30度角的直角三角形以及三角形的三边关系,解题的关键是找出当B'C最小时点B′的位置.本题属于中档题,难度不大,解决该题型题目时,根据三角形的三边关系确定点的位置是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
10.某校有甲、乙两个合唱队,两队队员的平均身高都为160cm,标准差分别是S甲、S乙,且S甲>S乙,则两个队的队员的身高较整齐的是( )
| A. | 甲队 | B. | 两队一样整齐 | C. | 乙队 | D. | 不能确定 |
12.某手机销售商分别以每部进价分别为800元、670元的A、B两种型号的手机,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的手机的销售单价;
(2)若手机销售商准备再采购这两种型号的手机共30台,且利润不低于4000元,求A种型号的手机至少能采购多少部?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 6台 | 7650元 |
| 第二周 | 4台 | 10台 | 11800元 |
(1)求A、B两种型号的手机的销售单价;
(2)若手机销售商准备再采购这两种型号的手机共30台,且利润不低于4000元,求A种型号的手机至少能采购多少部?
 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.
如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1. 如图,Rt△ABC中,∠C=90°,∠CAB=37°,AB=5,AC=4,BC=3,直线MN经过点C,交边AB于点D,分别过点A,B作AF⊥MN,BE⊥MN,垂足分别为点E,F,设线段BE,AF的长度分别为d1,d2.
如图,Rt△ABC中,∠C=90°,∠CAB=37°,AB=5,AC=4,BC=3,直线MN经过点C,交边AB于点D,分别过点A,B作AF⊥MN,BE⊥MN,垂足分别为点E,F,设线段BE,AF的长度分别为d1,d2.