题目内容
16. 如图,在?ABCD中,∠ABC=60°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F.
如图,在?ABCD中,∠ABC=60°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F.(1)求证:四边形BEDF是平行四边形;
(2)求∠FDC的大小.
分析 (1)根据平行四边形的性质得出AD∥BC,根据平行四边形的判定得出即可;
(2)求出∠EBF=30°,根据平行四边形的性质得出∠ADC=∠ABC=60°,∠EDF=∠EBF=30°,即可得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴ED∥BF,
∵DF∥BE,
∴四边形BEDF是平行四边形;
(2)解:∵∠ABC=60°,BE平分∠ABC,
∴∠EBF=$\frac{1}{2}$∠ABC=30°,
∵四边形BEDF是平行四边形,
∴∠EDF=∠EBF=30°,
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC=60°,
∴∠FDC=60°-30°=30°.
点评 本题考查了平行四边形的性质和判定的应用,能熟练地运用定理进行推理是解此题的关键,注意:平行四边形的对边互相平行,平行四边形的对角分别相等.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
4.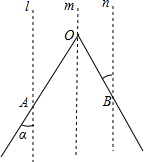 如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
 如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )| A. | 25° | B. | 45° | C. | 35° | D. | 30° |
5.下列选项是无理数的为( )
| A. | $-\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1 | D. | -π |
 如图,a∥b,∠1=76°,∠3=72°,则∠2的度数是32°.
如图,a∥b,∠1=76°,∠3=72°,则∠2的度数是32°. 如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)
如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)