题目内容
1. 如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)
如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{3}$,BC=1,以B为圆心,BC长为半径作弧,交AB于点D,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$(结果保留π)
分析 先根据锐角三角函数的定义求出∠B的度数,再根据S阴影=S△ABC-S扇形BCD进行解答即可.
解答 解:∵Rt△ABC中,∠C=90°,BC=1,AC=$\sqrt{3}$,
∴tanB=$\frac{AC}{BC}$=$\sqrt{3}$,
∴∠B=60°,
∴S阴影=S△ABC-S扇形BCD=$\frac{1}{2}$×$\sqrt{3}$×1-$\frac{60•π×{1}^{2}}{360}$=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$,
故答案为:$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
点评 本题考查的是扇形面积的计算及直角三角形的性质,熟知三角形及扇形的面积公式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知x+y=1,xy=-2,那么(2-x)(2-y)的值为( )
| A. | -3 | B. | -1 | C. | 0 | D. | 5 |
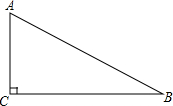 直角三角形ABC中,∠C=90°.
直角三角形ABC中,∠C=90°. 如图,在?ABCD中,∠ABC=60°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F.
如图,在?ABCD中,∠ABC=60°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F. 先阅读材料,解答下列问题:
先阅读材料,解答下列问题: