题目内容
9.甲、乙、丙三位同学站成一排,其中甲、乙两位同学相邻的概率是$\frac{2}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙两位同学相邻的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,其中甲、乙两位同学相邻的有4种情况,
∴甲、乙两位同学相邻的概率是:$\frac{4}{6}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20.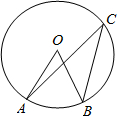 如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
 如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )| A. | 2π | B. | π | C. | $\frac{2}{3}$π | D. | $\frac{1}{3}$π |
17.甲、乙两组数据(单位:厘米)如下表
(1)根据以上数据填表(参考公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
(2)那一组数据比较稳定?
| 甲组 | 173 | 172 | 174 | 172 | 174 |
| 乙组 | 173 | 174 | 172 | 173 | 173 |
| 众数(单位:厘米) | 平均数(单位:厘米) | 方差(单位:厘米) | |
| 甲组 | 172 | 173 | 0.8 |
| 乙组 | 173 | 173 | 0.4 |
4.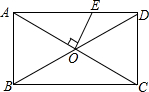 如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
 如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 1.5 |
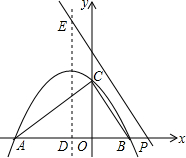 如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.
如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D. 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为8.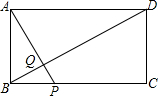 如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为t秒.
如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为t秒.