题目内容
12.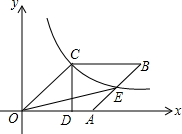 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为2$\sqrt{3}$-2.
如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为2$\sqrt{3}$-2.
分析 过E作EF垂直于x轴,由OD的长得到C的横坐标,代入反比例解析式求出纵坐标,确定出CD的长,利用勾股定理求出OC的长,即为OA的长,设EF=AF=x,表示出E坐标,代入反比例解析式求出x的值,确定出EF的长,即可求出三角形OAE面积.
解答 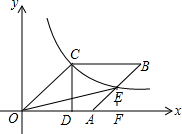 解:过点E作EF⊥x轴,交x轴于点F,
解:过点E作EF⊥x轴,交x轴于点F,
∵OD=2,即C横坐标为2,
∴把x=2代入反比例解析式得:y=2,即C(2,2),
∴CD=OD=2,即△OCD为等腰直角三角形,
∵四边形ABCO为菱形,
∴OC∥AB,OA=OC=2$\sqrt{2}$,
∴∠EAF=45°,
设EF=AF=x,则有OF=OA+AF=2$\sqrt{2}$+x,
∴E(2$\sqrt{2}$+x,x),
把E坐标代入反比例解析式得:x(2$\sqrt{2}$+x)=4,
解得:x=-$\sqrt{2}$+$\sqrt{6}$(负值舍去),
则△OAE面积S=$\frac{1}{2}$OA•EF=$\frac{1}{2}$×2$\sqrt{2}$×(-$\sqrt{2}$+$\sqrt{6}$)=2$\sqrt{3}{-}$2.
故答案为:2$\sqrt{3}$-2
点评 此题考查了菱形的性质,反比例函数图象上点的坐标特征,勾股定理,以及等腰直角三角形的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.若关于x的方程(m-2)x2+(3m-2)x+4m=0是一元一次方程,则m的值是( )
| A. | 0 | B. | $\frac{2}{3}$ | C. | 2 | D. | 任意有理数 |
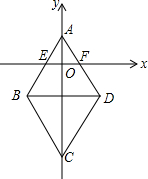 已知:如图,菱形ABCD中,已知点A(0,4)和C(0,-12),边AD交x轴于点F(3,0),求点B、D的坐标.
已知:如图,菱形ABCD中,已知点A(0,4)和C(0,-12),边AD交x轴于点F(3,0),求点B、D的坐标.