题目内容
7.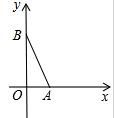 在平面直角坐标系中,A(2,0),∠BAO=75°,AB=6$\sqrt{2}$,以AB为斜边作等腰直角△ABC,如图所示,则C点坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).
在平面直角坐标系中,A(2,0),∠BAO=75°,AB=6$\sqrt{2}$,以AB为斜边作等腰直角△ABC,如图所示,则C点坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).
分析 分两种情况:①点C在第一象限,②点C在第二象限.针对每一种情况,分别画出图形,再利用解直角三角形求出距离,从而得出C点坐标.
解答 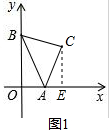 解:分两种情况:
解:分两种情况:
①如图1,过点C作CE⊥OA于E.
∵△ABC是等腰直角三角形,AB=6$\sqrt{2}$,
∴∠BAC=45°,AC=BC=6,
∵∠BAO=75°,
∴∠OAC=75°+45°=120°,
∴∠CAE=60°,
∴AE=3,CE=3$\sqrt{3}$,
∴OE=OA+AE=2+3=5,
则点C坐标为(5,3$\sqrt{3}$);
②如图2,过点C作CD⊥OA于D.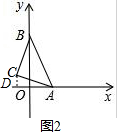
∵△ABC是等腰直角三角形,AB=6$\sqrt{2}$,
∴∠BAC=45°,AC=BC=6,
∵∠BAO=75°,
∴∠OAC=75°-45°=30°,
∴OD=$\frac{1}{2}$AC=3,OA=$\frac{\sqrt{3}}{2}$AC=3$\sqrt{3}$,
∴OE=AE-OA=3$\sqrt{3}$-2
∴点C坐标为(2-3$\sqrt{3}$,3).
综上可知点C坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).
故答案为:(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).
点评 考查了坐标与图形性质和等腰直角三角形性质,注意分类思想的运用,有一定的难度.

练习册系列答案
相关题目
17.将正整数1,2,3,…从小到大按下面规律排列,则第i行第j列的数为n(i-1)+j(用i,j表示).
| 第1列 | 第2列 | 第3列 | … | 第n列 | |
| 第1行 | 1 | 2 | 3 | … | n |
| 第2行 | n+1 | n+2 | n+3 | … | 2n |
| 第3行 | 2n+1 | 2n+2 | 2n+3 | … | 3n |
| … | … | … | … | … | … |
18.在-2,$\frac{1}{2}$,0,-$\frac{2}{3}$,-0.7,π,15%中,分数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是6.
如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是6. 如图,OB是∠AOC的平分线,∠2:∠3:∠4=2:3:5,求∠1,∠2,∠3,∠4的度数.
如图,OB是∠AOC的平分线,∠2:∠3:∠4=2:3:5,求∠1,∠2,∠3,∠4的度数.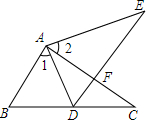 如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.