题目内容
19.若关于x的方程m-2(x-m)=4(m+1)-3x的解与关于x的方程$\frac{2x-m}{2}$-1=$\frac{4x+m}{3}$的解相同,则m的值为( )| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
分析 先分别求得两个方程的解(用含m的代数式表示),然后根据方程的解相同得到关于m的方程,从而可求得m的值.
解答 解:m-2(x-m)=4(m+1)-3x
去括号得:m-2x+2m=4m+4-3x
移项得:-2x+3x=4m+4-m-2m
合并同类项得:x=m+4.
$\frac{2x-m}{2}$-1=$\frac{4x+m}{3}$
去分母得:3(2x-m)-6=2(4x+m),
去括号得:6x-3m-6=8x+2m
移项得:6x-8x=2m+3m+6,
合并同类项得:-2x=5m+6,
系数化为1得;x=-$\frac{5m+6}{2}$.
∴-$\frac{5m+6}{2}$=m+4.
去分母得:-5m-6=2m+8,
移项得:-5m-2m=8+6,
合并同类项得:-7m=14,
系数化为1得:m=-2.
故选:B.
点评 本题主要考查的是同解方程的定义,掌握同解方程的定义和解一元一次方程的方法和步骤是解题的关键.

练习册系列答案
相关题目
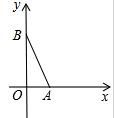 在平面直角坐标系中,A(2,0),∠BAO=75°,AB=6$\sqrt{2}$,以AB为斜边作等腰直角△ABC,如图所示,则C点坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).
在平面直角坐标系中,A(2,0),∠BAO=75°,AB=6$\sqrt{2}$,以AB为斜边作等腰直角△ABC,如图所示,则C点坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).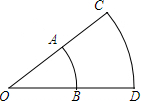 如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
 如图,在四边形ABCD中,AD∥BC,点E在AD上,且∠1=∠2,EB=ED,求证:四边形BCEF是菱形.
如图,在四边形ABCD中,AD∥BC,点E在AD上,且∠1=∠2,EB=ED,求证:四边形BCEF是菱形.