题目内容
12.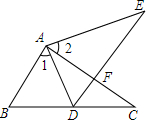 如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
分析 根据已知求得∠BAC=∠DAE,再由已知∠E=∠C,AE=AC,所以根据ASA可判定△ABC≌△ADE.
解答 证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{AC=AE}\\{∠C=∠E}\end{array}\right.$
∴△ABC≌△ADE(ASA).
点评 此题考查了全等三角形的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
相关题目
1.某公园的门票价格规定如下表:实验中学组织七年级两个班到这个公园郊游,两班共有学生104人,其中(一)班不足50人,(二)班多于50人,购买门票时,若两个班各自统一购票,则需1136元;若两个班合在一起购票,就可以节省一部分钱.
(1)两班各有学生多少人?
(2)两个班合在一起购票比两个班各自统一购票分别节省多少钱?
| 购票人数/人 | 1~50 | 51~100 | 100以上 |
| 每人票价/元 | 12 | 10 | 8 |
(2)两个班合在一起购票比两个班各自统一购票分别节省多少钱?
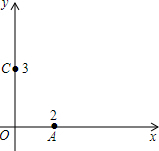 已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).
已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).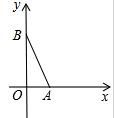 在平面直角坐标系中,A(2,0),∠BAO=75°,AB=6$\sqrt{2}$,以AB为斜边作等腰直角△ABC,如图所示,则C点坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).
在平面直角坐标系中,A(2,0),∠BAO=75°,AB=6$\sqrt{2}$,以AB为斜边作等腰直角△ABC,如图所示,则C点坐标为(5,3$\sqrt{3}$)和(2-3$\sqrt{3}$,3).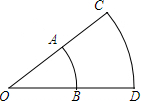 如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长. 如图,已知线段a、b,求作线段AB,使得AB=2b-a(不写作法).
如图,已知线段a、b,求作线段AB,使得AB=2b-a(不写作法).