题目内容
1.如果2a+b=0,则|$\frac{a}{|b|}$-1|+|$\frac{|a|}{b}$-2|=3.分析 根据2a+b=0,得a,b异号且b=-2a,代入原式根据绝对值性质分①a>0、b<0和②a<0、b>0两种情况求解即可.
解答 解:∵2a+b=0,
∴a,b异号,且b=-2a,
当a>0时,b=-2a<0,
∴原式=|$\frac{a}{|-2a|}$-1|+|$\frac{|a|}{-2a}$-2|
=|$\frac{a}{2a}$-1|+|$\frac{a}{-2a}$-2|
=|$\frac{1}{2}$-1|+|-$\frac{1}{2}$-2|
=$\frac{1}{2}$+$\frac{5}{2}$
=3;
当a<0时,b=-2a>0,
原式=|$\frac{a}{-2a}$-1|+|$\frac{-a}{-2a}$-2|
=|-$\frac{1}{2}$-1|+|$\frac{1}{2}$-2|
=$\frac{3}{2}$+$\frac{3}{2}$
=3,
故答案为:3.
点评 本题主要考查绝对值,熟练掌握①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
11.把弯曲的公路改直,能够缩短行程,这样的道理是( )
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 两点之间线段最短 | D. | 两点之间直线最短 |
6.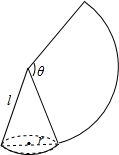 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )
如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长为( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
 如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色)小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.
如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色)小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.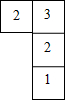 若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数.
若一个几何体由几个大小相同的小正方体搭成,每个小正方体的棱长为1cm.从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小正方体的个数. 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E,⊙O的切线BF与弦AD的延长线相交于点F,且OA=3,BE=2.