题目内容
15．
如图，一把直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=120°，求∠CBE的度数．
分析 先根据补角的定义求出∠ADB的度数，再由平行线的性质即可得出结论．
解答 解：∵∠ADE=120°
∴∠ADB=180°-∠ADE=60°．
∵EF∥BC，
∴∠CBE=∠ADB=60°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．
练习册系列答案
相关题目
如图，△ABC中，AB=6cm，AC=5cm，BC=7cm，BD平分∠ABC，CE平分∠ACB，AD⊥BD，AE⊥CE，则DE=2cm．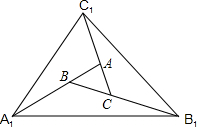
如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB、BC、CA至点A1、B1、C1，使得A1B=AB，B1C=BC，C1A=CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1；第二次操作，分别延长A1B1，B1C1，C1A1至A2，B2，C2，使得A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，记其面积为S2…，按此规律继续下去．第n次操作得到△AnBnCn，则S1=7，△AnBnCn的面积Sn=7n．
20．下列各组数中，是方程2x+3y=7的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$ |
5．
如图，已知△ABC是腰长为1的等腰直角三形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第2015个等腰直角三角形的斜边长是（ ）
如图，已知△ABC是腰长为1的等腰直角三形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第2015个等腰直角三角形的斜边长是（ ）| A． | ${（{\sqrt{2}}）^{2014}}$ | B． | ${（{\sqrt{2}}）^{2015}}$ | C． | 22014 | D． | 22015 |