题目内容
10.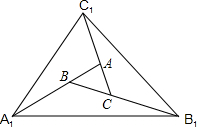 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.
分析 利用三角形同高等底面积相等,进而求出,得出规律解答即可.
解答 解:∵B1C=BC,A1B=AB,
∴S△ABC=S△BCA1,S△BCA1=S△A1CB1,
∴S△A1B1C=2S△ABC=2a,
同理可得出:S△A1AC1=S△CB1C1=2,
∴S1=2a+2a+2a+a=7;,△AnBnCn的面积Sn=7n
故答案为:7;7n.
点评 此题主要考查了面积及等积变换,利用三角形同高则面积比与底边关系分别分析得出是解题关键.

练习册系列答案
相关题目
1.下列叙述正确的是( )
| A. | a>b,则ac2>bc2 | B. | 当x<7时,3(x-7)是负数 | ||
| C. | 若-$\frac{x}{3}$<0,则x>-3 | D. | 当x<0时,x2<3x |
2.下列说法正确的是( )
| A. | 旋转对称图形都是中心对称图形 | |
| B. | 角的对称轴就是它的角平分线 | |
| C. | 直角三角形三条高的交点就是它的直角顶点 | |
| D. | 钝角三角形的三条高(或所在直线)的交点在三角形的内部 |
 如图,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为点F,连接OF.求:
如图,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为点F,连接OF.求: 如图(1),四边形ABCD是一张边长为2a的正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使点B落在EF上,对应点为B′.
如图(1),四边形ABCD是一张边长为2a的正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使点B落在EF上,对应点为B′. 如图,一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=120°,求∠CBE的度数.
如图,一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=120°,求∠CBE的度数. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数.
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数. 如图,是由4个完全相同的小正方体组成的立体图形,它的主视图是( )
如图,是由4个完全相同的小正方体组成的立体图形,它的主视图是( )


