题目内容
9．满足下列条件：①a=2，b=3，c=4；②a=3，b=5，c=2；③a：b：c=1：2：3；④a=m+1，b=n+2，c=2m（m＞2）的三条线段a、b、c，能组成三角形的有（ ）| A． | ①② | B． | ③④ | C． | ①④ | D． | ①③ |
分析 根据三角形三边关系定理：三角形两边之和大于第三边进行分析即可．
解答 解：①∵2+3＞4，∴能组成三角形；
②∵2+3=5，∴不能组成三角形；
③∵1+2=3，∴不能组成三角形；
④∵m+1+m+2＞2m，∴能组成三角形；
故选：C．
点评 此题主要考查了三角形的三边关系定理，在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．
练习册系列答案
相关题目
17．
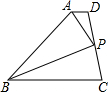如图，已知四边形ABCD中，AD∥BC，AP平分∠DAB，BP平分∠ABC，它们的交点P给在线段CD上，下面的结论：①AP⊥BP；②点P到直线AD、BC的距离相等；③PD=PC．其中正确的结论有（ ）
如图，已知四边形ABCD中，AD∥BC，AP平分∠DAB，BP平分∠ABC，它们的交点P给在线段CD上，下面的结论：①AP⊥BP；②点P到直线AD、BC的距离相等；③PD=PC．其中正确的结论有（ ）| A． | ①②③ | B． | ①② | C． | 仅① | D． | 仅② |
1．在平面直角坐标系中，已知点A（-4，2），B（-6，-4），以原点O为位似中心，相似比为$\frac{1}{2}$，把△ABO缩小，则点A的对应点A′的坐标是（ ）
| A． | （-2，1） | B． | （-8，4） | C． | （-2，1）或（2，-1） | D． | （-8，4）或（8，-4） |
18．如果单项式-5xa+1y4与2ybx3是同类项，那么a、b的值分别是（ ）
| A． | a=1，b=4 | B． | a=1，b=3 | C． | a=2，b=4 | D． | a=2，b=3 |
19．一元二次方程x2-mx-2=0的一个根为2，则m的值是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |