题目内容
14.一元钱硬币的直径约为24mm,则用它能完全覆盖住的正六边形的边长最大不能超过12mm.分析 根据题意得出圆内接半径r为12mm,则OB=12,求得BD=OB•sin30°,则BC=2BD,即可得出结果.
解答 解:根据题意得:圆内接半径r为12mm,如图所示: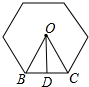
则OB=12,
∴BD=OB•sin30°=12×$\frac{1}{2}$=6(mm),
则BC=2×6=12(cm),
完全覆盖住的正六边形的边长最大为12mm.
故答案为:12mm.
点评 本题考查了正多边形和圆、正六边形的性质、三角函数、等腰三角形的性质等知识;运用三角函数求出圆内接正六边形的边长是解决问题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.满足下列条件:①a=2,b=3,c=4;②a=3,b=5,c=2;③a:b:c=1:2:3;④a=m+1,b=n+2,c=2m(m>2)的三条线段a、b、c,能组成三角形的有( )
| A. | ①② | B. | ③④ | C. | ①④ | D. | ①③ |
19.下列四个点,在反比例函数y=$\frac{12}{x}$图象上的是( )
| A. | (2,-6) | B. | (8,4) | C. | (3,-4) | D. | (-6,-2) |
6.若分式$\frac{{x}^{2}-9}{3x+9}$的值为0,则x的值为( )
| A. | 3 | B. | -3 | C. | x=±3 | D. | x≠-3 |
 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25m,与亭子距离CE=20m,小丽从楼房顶测得E点的俯角为45°.求:
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25m,与亭子距离CE=20m,小丽从楼房顶测得E点的俯角为45°.求: