题目内容
11.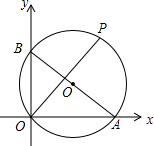 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )| A. | (8,6) | B. | (7,7) | C. | (7$\sqrt{2}$,7$\sqrt{2}$) | D. | (5$\sqrt{2}$,5$\sqrt{2}$) |
分析 作PH⊥x轴于H,连结PA、PB,由A、B两点的坐标可求出AB,由△PAB和△POH都为等腰直角三角形,得出PA=$\frac{\sqrt{2}}{2}$AB,PH=OH,设OH=t,在在Rt△PHA中,运用勾股定理求出t的值,即可得出点P的坐标.
解答  解:如图,作PH⊥x轴于H,连结PA、PB,
解:如图,作PH⊥x轴于H,连结PA、PB,
∵∠AOB=90°,
∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵A、B两点的坐标分别为(8,0)、(0,6),
∴OA=8,OB=6,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10,
∵∠AOP=45°,
∴∠ABP=45°,
∴△PAB和△POH都为等腰直角三角形,
∴PA=$\frac{\sqrt{2}}{2}$AB=5$\sqrt{2}$,PH=OH,
设OH=t,则PH=t,AH=8-t,
在Rt△PHA中,
∵PH2+AH2=PA2,即t2+(8-t)2=(5$\sqrt{2}$)2,
解得t1=7,t2=1(舍去),
∴P点坐标为(7,7).
故选B.
点评 本题考查的是圆周角定理及等腰直角三角形的性质,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
6.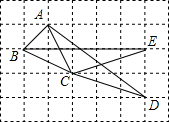 如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
 如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )
如图,在边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上.则tan∠ADC的值等于( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |
 如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为112.5°.
如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为112.5°.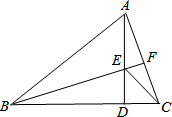 在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,求证:
在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,求证: