题目内容
16.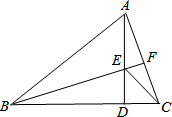 在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,求证:
在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,求证:(1)△ADC≌△BDE;
(2)EA=EC.
分析 (1)直接利用全等三角形的判定方法得出答案;
(2)由条件可求得∠BAC=∠BCA=67.5°,且∠BAD=∠DCE=45°,可得∠EAC=∠ECA=22.5°,可证得结论.
解答 证明:(1)∵AD⊥BC,∠ABC=45°,
∴AD=BD,
在△ADC和△BDE中,
$\left\{\begin{array}{l}{AD=BD}\\{∠CDA=∠EDB}\\{DC=DE}\end{array}\right.$,
∴△ADC≌△BDE(SAS);
(2)∵BA=BC,∠ABC=45°,
∴∠BCA=∠BAC=$\frac{1}{2}$×135°=67.5°,
又∵AD⊥BC,
∴∠ADC=90°,
∵ED=CD,
∴∠ECD=45°,
∴∠ACE=67.5°-45°=22.5°,
∵∠AEC=∠EDC+∠ECD=135°,
∴∠EAC=180°-22.5°-135°=22.5°,
∴EA=EC.
点评 本题主要考查了全等三角形的判定以及等腰三角形的性质,由条件分别计算出∠ACE和∠EAC的度数是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
11.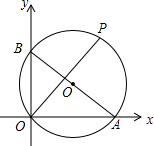 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )| A. | (8,6) | B. | (7,7) | C. | (7$\sqrt{2}$,7$\sqrt{2}$) | D. | (5$\sqrt{2}$,5$\sqrt{2}$) |
 如图,在两个同心圆中,AB、CD分别是大圆和小圆的直径.求证:四边形ACBD是平行四边形.
如图,在两个同心圆中,AB、CD分别是大圆和小圆的直径.求证:四边形ACBD是平行四边形.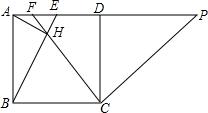 如图,在正方形ABCD中,E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F,CP⊥CF交AD的延长线于点P,若EF=1,则DP的长为$\frac{16}{3}$.
如图,在正方形ABCD中,E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F,CP⊥CF交AD的延长线于点P,若EF=1,则DP的长为$\frac{16}{3}$.
 如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=52°,CE⊥AD,则∠DCE的度数是64°.
如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=52°,CE⊥AD,则∠DCE的度数是64°.