题目内容
11.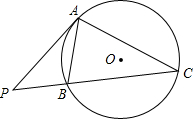 如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线.
如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线.
分析 过点A作直径AD,连结BD,如图,利用圆周角定理得到∠D+∠BAD=90°,∠C=∠D,加上∠PAB=∠C,则∠PAB+∠BAD=90°,所以AD⊥PA,然后根据切线的判定定理即可得到结论.
解答 证明:过点A作直径AD,连结BD,如图,
∵AD为直径,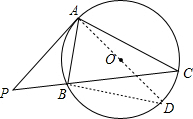
∴∠ABDF=90°,
∴∠D+∠BAD=90°,
∵∠C=∠D,∠PAB=∠C,
∴∠D=∠PAB,
∴∠PAB+∠BAD=90°,即∠PAD=90°,
∴AD⊥PA,
∴PA是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.解决问题的关键是构建以AD为直径的直角三角形.

练习册系列答案
相关题目
2.已知$\sqrt{x}$=6.5012,650.12=$\sqrt{422630}$,则x=( )
| A. | 4226.3 | B. | 42.263 | C. | 0.042263 | D. | 42263000 |
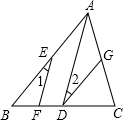 已知:如图,AD∥EF,∠1=∠2,判断AB与DG的位置关系,并说明理由.
已知:如图,AD∥EF,∠1=∠2,判断AB与DG的位置关系,并说明理由. 如图,已知⊙O的半径OA=3,PA是⊙O的切线,A为切点,PO交⊙O于点B,PA=4,求PB的长.
如图,已知⊙O的半径OA=3,PA是⊙O的切线,A为切点,PO交⊙O于点B,PA=4,求PB的长.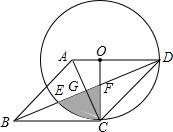 如图,已知菱形ABCD中,AD∥BC,AD=$\sqrt{2}$,点O是AD上一点,以O为圆心,OD长为半径的⊙O与BC相切于点C,与BD相交于点E,连接OC,AC,分别与BD相交于点F,G.
如图,已知菱形ABCD中,AD∥BC,AD=$\sqrt{2}$,点O是AD上一点,以O为圆心,OD长为半径的⊙O与BC相切于点C,与BD相交于点E,连接OC,AC,分别与BD相交于点F,G.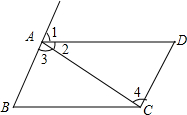 如图,由下列条件可以判定图中哪两条直线平行,说明理由
如图,由下列条件可以判定图中哪两条直线平行,说明理由 如图,l1∥l2,∠ABC=120°,l1⊥AB.
如图,l1∥l2,∠ABC=120°,l1⊥AB.