题目内容
6. 如图,已知⊙O的半径OA=3,PA是⊙O的切线,A为切点,PO交⊙O于点B,PA=4,求PB的长.
如图,已知⊙O的半径OA=3,PA是⊙O的切线,A为切点,PO交⊙O于点B,PA=4,求PB的长.
分析 根据切线的性质,在RT△PAO中利用勾股定理即可解决问题.
解答 解: ∵PA是切线,点A是切点,
∵PA是切线,点A是切点,
∴OA⊥PA,
∴∠PAO=90°,
∵PA=4,AO=3,
∴PO=$\sqrt{A{P}^{2}+A{O}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴PB=PO-OB=5-3=2.
点评 本题考查切线的性质、勾股定理等知识,掌握切线垂直于过切点的半径是解决问题的关键,属于基础题目,中考常考题型.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
17.已知正方形的边长为a,面积为S,则( )
| A. | a=$\sqrt{S}$ | B. | a=$\sqrt{S}$ | C. | S=$\sqrt{a}$ | D. | S=±$\sqrt{a}$ |
18.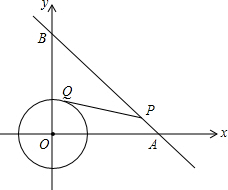 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
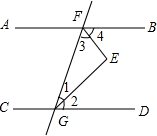 如图,∠1=∠2,∠3=∠4,且∠2+∠3=90°,试说明AB∥CD.
如图,∠1=∠2,∠3=∠4,且∠2+∠3=90°,试说明AB∥CD.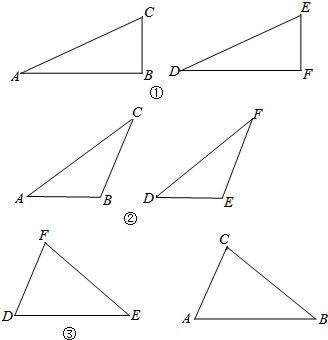
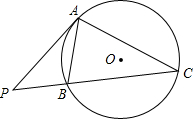 如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线.
如图,⊙O为△ABC的外接圆,点P为CB延长线上一点,且∠PAB=∠C.求证:PA是⊙O的切线. 如图,已知∠1=∠2,BD平分∠ABC,可得到那两条直线平行?如果要得到另外两条直线平行,则应将上述两个条件之一做如何改变?
如图,已知∠1=∠2,BD平分∠ABC,可得到那两条直线平行?如果要得到另外两条直线平行,则应将上述两个条件之一做如何改变?