题目内容
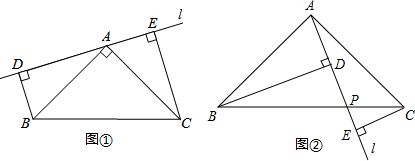
如图①,在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,且BD⊥l于的D,CE⊥l于的E.
(1)求证:BD+CE=DE;
(2)当变换到如图②所示的位置时,试探究BD、CE、DE的数量关系,请说明理由.
(1)求证:BD+CE=DE;
(2)当变换到如图②所示的位置时,试探究BD、CE、DE的数量关系,请说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)易证∠EAC=∠ABD,即可求证△ABD≌△CAE,根据全等三角形相等的性质即可解题;
(2)先根据垂直的定义得到∠AEC=∠BDA=90°,再根据等角的余角相等得到∠ABD=∠CAE,则可利用“AAS”判断△ABD≌△CAE,所以AD=CE,BD=AE,于是有BD-CE=AE-AD=DE.
(2)先根据垂直的定义得到∠AEC=∠BDA=90°,再根据等角的余角相等得到∠ABD=∠CAE,则可利用“AAS”判断△ABD≌△CAE,所以AD=CE,BD=AE,于是有BD-CE=AE-AD=DE.
解答:
证明:(1)∵∠DAB+∠EAC=90°,∠DAB+∠ABD=90°,
∴∠EAC=∠ABD,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=AD,
∵DE=AD+AE,
∴DE=BD+CE;
(2)BD-CE=DE,
理由如下:
∵CE⊥AN,BD⊥AN,
∴∠AEC=∠BDA=90°,
∴∠BAD+∠ABD=90°,
∵∠BAC=90°,即∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,
∴BD-CE=AE-AD=DE.
∴∠EAC=∠ABD,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=AD,
∵DE=AD+AE,
∴DE=BD+CE;
(2)BD-CE=DE,
理由如下:
∵CE⊥AN,BD⊥AN,
∴∠AEC=∠BDA=90°,
∴∠BAD+∠ABD=90°,
∵∠BAC=90°,即∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,
∴BD-CE=AE-AD=DE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等,本题中求证△ABD≌△CAE是解题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图所示,△ABC中,AB=BC=AC,BD=CE,AD与BE相交于点P,则∠APE的度数是( )| A、45° | B、55° |
| C、75° | D、60° |
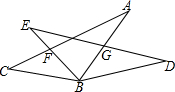 如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )
如图,BC=BE,∠C=∠E,∠CBE=∠ABD,则下列结论错误的是( )| A、∠A=∠D |
| B、BF=BG |
| C、AC=DE |
| D、BA=BD |
 如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,点A落在平面内的A′处,若∠BDA′=70°,则∠B的度数是
如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,点A落在平面内的A′处,若∠BDA′=70°,则∠B的度数是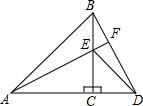 如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.
如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.