题目内容
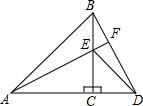 如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.
如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F.(1)求证:AE=BD;
(2)试判断直线AE与BD的位置关系,并证明你的结论.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据SAS判定△ACE≌△BCD,从而得到∠EAC=∠DBC,根据角之间的关系可证得AF⊥BD.
(2)互相垂直,只要证明∠AFD=90°,从而转化为证明∠EAC+∠CDB=90°即可.
(2)互相垂直,只要证明∠AFD=90°,从而转化为证明∠EAC+∠CDB=90°即可.
解答:
(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACE=∠BCD=90°,
在△ACE和△BCD,
∴△ACE≌△BCD(SAS);
(2)答:直线AE与BD互相垂直,理由为:
证明:∵△ACE≌△BCD,
∴∠EAC=∠DBC,
又∵∠DBC+∠CDB=90°,
∴∠EAC+∠CDB=90°,
∴∠AFD=90°,
∴AF⊥BD,
即直线AE与BD互相垂直.
∴AC=BC,CE=CD,∠ACE=∠BCD=90°,
在△ACE和△BCD,
|
∴△ACE≌△BCD(SAS);
(2)答:直线AE与BD互相垂直,理由为:
证明:∵△ACE≌△BCD,
∴∠EAC=∠DBC,
又∵∠DBC+∠CDB=90°,
∴∠EAC+∠CDB=90°,
∴∠AFD=90°,
∴AF⊥BD,
即直线AE与BD互相垂直.
点评:此题主要考查学生对全等三角形的判定及直角三角形的判定的掌握情况.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、-(-42)=-16 | ||||||||
| B、-8-2×6=(-1+6)×(-2) | ||||||||
C、4÷
| ||||||||
| D、(-1)2013+(-1)2014=-1+1=0 |
 如图,在矩形ABCD中,点E为CD上一点,且AE=AB,连BE,求证:∠BAE=2∠CBE.
如图,在矩形ABCD中,点E为CD上一点,且AE=AB,连BE,求证:∠BAE=2∠CBE.