题目内容

5．把二次根式（x-1）$\sqrt{\frac{1}{1-x}}$化简为最简二次根式，结果正确的是（　　）
A．$\sqrt{1-x}$B．-$\sqrt{1-x}$C．-$\sqrt{x-1}$D．$\sqrt{x-1}$

分析 直接利用二次根式的性质得出x-1＜0，进而化简求出答案．

解答 解：∵$\sqrt{\frac{1}{1-x}}$有意义，
∴1-x＞0，
∴x-1＜0，
∴（x-1）$\sqrt{\frac{1}{1-x}}$=-$\sqrt{（1-x）^{2}×\frac{1}{1-x}}$=-$\sqrt{1-x}$．
故选：B．

点评 此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．

练习册系列答案
相关题目
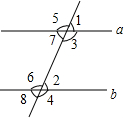15．如图，在条件：①∠5=∠6，②∠7=∠2，③∠3+∠8=180°，④∠3=∠2，⑤∠4+∠1=180°中，能判定a∥b的条件有（　　）
A．4个B．3个C．2个D．1个
16．你能求（x-1）（x99+x98+x97+…+x+1）的值吗？遇到这样的问题，我们可以先思考一下，从简单的情形入手．先分别计算下列各式的值：
①（x-1）（x+1）=x2-1；
②（x-1）（x2+x+1）=x3-1；
③（x-1）（x3+x2+x+1）=x4-1；
…
由此我们可以得到：（x-1）（x99+x98+x97+…+x+1）=x100-1．
请你利用上面的结论，再完成下面两题的计算：
（1）（-2）50+（-2）49+（-2）48+…+（-2）+1．
（2）若x3+x2+x+1=0，求x2016的值．
13．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于点H，连接OH．
（1）求AD与DH的长；
（2）求证：∠HDO=∠DCO．
20．如图，在平面直角坐标系中，已知A，B，C三点的坐标分别为（0，a）（b，0）（b，c）（如图所示），其中a，b，c满足关系式（a-2）2+$\sqrt{b-3}$=0，|c-4|≤0．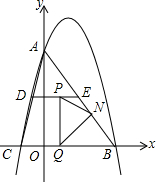
（1）求a，b，c的值；
（2）如果在第二象限内有一点P（m，1），请用含m的代数式表示△AOP的面积；
（3）在（2）的条件下，是否存在点P，使△AOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．
10．方程2xn-3-y3m+n-2+3=0是二元一次方程，则3m-n=-5．
17．如图，已知抛物线y=-$\frac{4}{3}$x2+bx+c经过A（0，4），B（3，0）两点，与x轴负半轴交于点C，连接AC、AB．
（1）求该抛物线的解析式；
（2）D、E分别为AC、AB的中点，连接DE，P为DE上的动点，PQ⊥BC，垂足为Q，QN⊥AB，垂足为N，连接PN．
①当△PQN与△ABC相似时，求点P的坐标；
②是否存在点P，使得PQ=NQ，若存在，直接写出点P的坐标，若不存在，请说明理由．
14．若（x+3）（x+n）=x2+mx-15，则m的值为（　　）
A．-5B．-2C．5D．2
15．不等式4+2x＞0的解集是（　　）
A．2x＞4B．x＞2C．x＞-2D．x＜-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网