题目内容
17.设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于任何一个二次函数,它在给定的闭区间上都有最小值.(1)函数y=-x2+4x-2在区间[0,5]上的最小值是-7
(2)求函数$y={({x+\frac{1}{2}})^2}+\frac{3}{4}$在区间$[{0,\frac{3}{2}}]$上的最小值.
(3)求函数y=x2-4x-4在区间[t-2,t-1](t为任意实数)上的最小值ymin的解析式.
分析 (1)先求得抛物线的对称轴、顶点坐标,然后画出抛物线的大致图象,根据函数图象可知当x=-5时,函数值最小;
(2)先画出函数的大致图象,然后根据函数图象可知当x=0时,函数值最小;
(3)先求得抛物线的对称轴,然后根据抛物线的对称轴在区间[t-2,t-1]的左侧、区间内、区间右侧分类讨论即可.
解答 解:(1)y=-x2+4x-2其对称轴为直线为x=2,顶点坐标为(2,2),函数图象开口向下.
函数图大致象如图1所示:
当x=5时,函数有最小值,最小值为-7.
故答案为:-7.
(2)$y={({x+\frac{1}{2}})^2}+\frac{3}{4}$,其对称轴为直线$x=-\frac{1}{2}$,顶点坐标$({-\frac{1}{2},\frac{3}{4}})$,且图象开口向上.
其顶点横坐标不在区间$[{0,\frac{3}{2}}]$内,
如图2所示.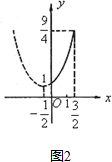
当x=0时,函数y有最小值$y_{min}^{\;}=1$.
(3)将二次函数配方得:y=x2-4x-4=(x-2)2-8
其对称轴为直线:x=2,顶点坐标为(2,-8),图象开口向上
若顶点横坐标在区间[t-2,t-1]左侧,则2<t-2,即t>4.
当x=t-2时,函数取得最小值:${y_{min}}={(t-4)^2}-8={t^2}-8t+8$
若顶点横坐标在区间[t-2,t-1]上,则t-2≤2≤t-1,即3≤t≤4.
当x=2时,函数取得最小值:ymin=-8
若顶点横坐标在区间[t-2,t-1]右侧,则t-1<2,即t<3.
当x=t-1时,函数取得最小值:${y_{min}}={(t-3)^2}-8={t^2}-6t+1$
综上讨论,得${y_{min}}=\left\{\begin{array}{l}{t^2}-8t+8(t>4)\\-8(3≤t≤4)\\{t^2}-6t+1(t<3)\end{array}\right.$.
点评 本题主要考查的是二次函数的最值,根据函数解析式画出函数的图象,然后根据对称轴是否在区间内进行分类讨论是解题的关键.

| 甲 | 5.05 | 5.02 | 5 | 4.96 | 4.97 |
| 乙 | 5 | 5.01 | 5 | 4.97 | 5.02 |
 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
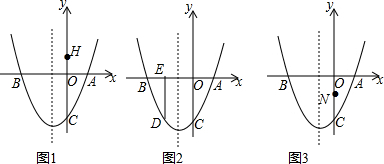
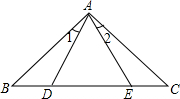 如图,AB=AC,∠1=∠2,AD=AE,则BD=CE.
如图,AB=AC,∠1=∠2,AD=AE,则BD=CE.