题目内容
7.某工厂为了选拔1名车工参加直径为5mm精密零件的加工技术比赛,随机抽取甲,乙两名车工加工的5个零件.现测得的结果如表.平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,方差依次为S甲2,S乙2,则$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,S甲2>S乙2(填入“=”或“>”或“<”).| 甲 | 5.05 | 5.02 | 5 | 4.96 | 4.97 |
| 乙 | 5 | 5.01 | 5 | 4.97 | 5.02 |
分析 求出甲中样本数据的和再除以5可得平均数,再求出乙中样本数据的和再除以5可得平均数,然后比较即可;
利用方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],分别计算出甲和乙的方差即可.
解答 解:∵$\overline{{x}_{甲}}$=(5.05+5.02+5+4.96+4.97)÷5=5,
$\overline{{x}_{乙}}$=(5+5.01+5+4.97+5.02)÷5=5,
∴$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,
∵${{S}_{甲}}^{2}$=$\frac{1}{5}$[(5.05-5)2+(5.02-5)2+((5-5)2+(4.96-5)2+(4.97-5)2]=0.00108,
${{S}_{乙}}^{2}$=$\frac{1}{5}$[(5-5)2+(5.01-5)2+((5-5)2+(4.97-5)2+(5.02-5)2]=0.00028,
∴S甲2>S乙2,
故答案为:=;>.
点评 此题主要考查了算术平均数和方差,关键是掌握方差的计算公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

练习册系列答案
相关题目
17.从A、B、C三张卡片中任取两张,取到A、B的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2.如果+50m表示向东走50m,那么向西走40m表示为( )
| A. | -50m | B. | -40m | C. | +40m | D. | +50m |
12.近几年安徽省民生事业持续改善,2012年全省民生支出3163亿元,2014年全省民生支出4349亿元,若平均每年民生支出的增长率相同,设这个增长率为x,则下列列出的方程中正确的是( )
| A. | 3163(1+x)2=4349 | B. | 4349(1-x)2=3163 | C. | 3163(1+2x)=4349 | D. | 4349(1-2x)=3163 |
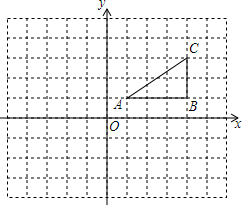 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC:
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC: