题目内容
5.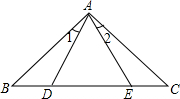 如图,AB=AC,∠1=∠2,AD=AE,则BD=CE.
如图,AB=AC,∠1=∠2,AD=AE,则BD=CE.
分析 依据SAS可证明△ABD≌△ACE,然后由全等三角形的性质可知BD=EC.
解答 解:∵在△ABD和△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠1=∠2}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE.
∴BD=CE.
故答案为:CE.
点评 本题主要考查的是全等三角形的性质和判定,证得△ABD≌△ACE是解题的关键.

练习册系列答案
相关题目
13.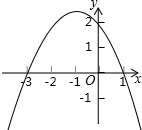 抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )
抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )
 抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )
抛物线y=ax2+bx+c的图象如图所示,则使得y>0的x的取值范围是( )| A. | x<2 | B. | x>-3 | C. | -3<x<1 | D. | x<-3或x>1 |
8.关于x的方程x2+2x-k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<1 | D. | k<1且k≠0 |
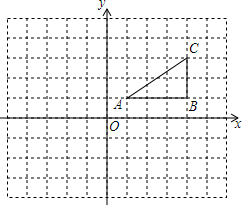 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC:
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC: 如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).
如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).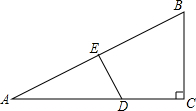 已知,如图,在Rt△ABC中,斜边AB的垂直平分线分别交AC,AB于点D,E,AE=BC,求证:AD=2CD.
已知,如图,在Rt△ABC中,斜边AB的垂直平分线分别交AC,AB于点D,E,AE=BC,求证:AD=2CD.