Question

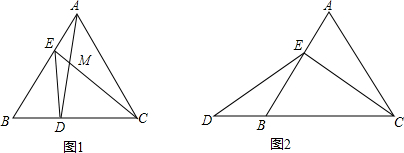
12．如图1，在等边△ABC中，点E从顶点A出发，沿AB的方向运动，同时，点D从顶点B出发，沿BC的方向运动，它们的速度相同，当点E到达点B时，D、E两点同时停止运动．
（1）求证：CE=AD；
（2）连接AD、CE交于点M，则在D、E运动的过程中，∠CMD变化吗？若变化，则说明理由；若不变，则求出它的度数；
（3）如图2，若点D从顶点B出发后，沿BC相反的方向运动，其它条件不变．求证：CE=DE．

Answer 1

分析 （1）根据等边三角形的性质得△CAE≌△ABD，从而得证；
（2）由（1）中全等得到结果；
（3）过点E作EF平行于BC交AC于点F，易证△AEF为等边三角形，由此得到△CFE≌△EBD，从而得证．

解答 （1）证明：∵△ABC为等边三角形，
∴∠CAE=∠ABD=60°，
在△CAE和△ABD中，
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠ABD}\\{AE=BD}\end{array}\right.$，
∴△CAE≌△ABD，
∴CE=AD；
（2）解：∠CMD的大小不变，
∵△CAE≌△ABD，
∴∠ACE=∠BAD，
∵∠CAD+∠BAD=∠BAC=60°，
∴∠CMD=∠CAD+∠ACE=∠CAD+∠BAD=60°；
（3）证明：如图，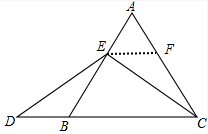

过点E作EF∥BC交AC于点F，
则∠AEF=∠ABC=60°，∠AFE=∠ACB=60°，△AEF为等边三角形，
在△CFE和△EBD中，
$\left\{\begin{array}{l}{EF=AE=BD}\\{∠EFC=∠DBE=120°}\\{CF=EB}\end{array}\right.$，
∴△CFE≌△EBD，
∴CE=DE．

点评 此题考查三角形全等的判定与性质，等边三角形的性质，掌握三角形全等的判定方法是解决问题的关键．