题目内容
14.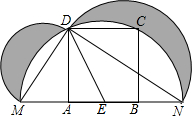 如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )| A. | 9$\sqrt{5}$ | B. | 18$\sqrt{5}$ | C. | 36$\sqrt{5}$ | D. | 72$\sqrt{5}$ |
分析 根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积,MN的半圆的直径,从而可知∠MDN=90°,在Rt△MDN中,由勾股定理可知:MN2=MD2+DN2,从而可得到两个小半圆的面积=大半圆的面积,故此阴影部分的面积=△DMN的面积,在Rt△AED中,DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,所以MN=6$\sqrt{5}$,然后利用三角形的面积公式求解即可.
解答 解:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积.
∵MN是半圆的直径,
∴∠MDN=90°.
在Rt△MDN中,MN2=MD2+DN2,
∴两个小半圆的面积=大半圆的面积.
∴阴影部分的面积=△DMN的面积.
在Rt△AED中,DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴阴影部分的面积=△DMN的面积=$\frac{1}{2}MN•AD$=$\frac{1}{2}×6\sqrt{5}×6=18\sqrt{5}$.
故选:B.
点评 本题主要考查的是求不规则图形的面积,将不规则图形的面积转化为规则图形的面积是解答此类问题的常用方法,发现阴影部分的面积=△DMN的面积是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
19.以下问题,不适合用全面调查的是( )
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对招聘人员的面试 | ||
| C. | 了解一批灯泡的使用寿命 | D. | 了解701班的身高情况 |
4.“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为$\frac{1}{3}$.
(2)为估算本次赛事参加“迷你马拉松”的人数,小明对部分参赛选手作如下调查:
①请估算本次赛事参加“迷你马拉松”人数的概率为0.4.(精确到0.1)
②若本次参赛选手大约有30000人,请你估计参加“迷你马拉松”的人数是多少?
(1)小明被分配到“迷你马拉松”项目组的概率为$\frac{1}{3}$.
(2)为估算本次赛事参加“迷你马拉松”的人数,小明对部分参赛选手作如下调查:
| 调查总人数 | 50 | 100 | 200 | 500 | 1000 |
| 参加“迷你马拉松”人数 | 21 | 45 | 79 | 200 | 401 |
| 参加“迷你马拉松”频率 | 0.360 | 0.450 | 0.395 | 0.400 | 0.401 |
②若本次参赛选手大约有30000人,请你估计参加“迷你马拉松”的人数是多少?
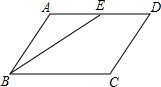 如图,在平行四边形ABCD中,点E为AD的中点,试用无刻度的直尺分别在四边形的内部和外部各画一个与△ABE全等的三角形.
如图,在平行四边形ABCD中,点E为AD的中点,试用无刻度的直尺分别在四边形的内部和外部各画一个与△ABE全等的三角形. 如图,?ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则?ABCD的面积等于4.
如图,?ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则?ABCD的面积等于4.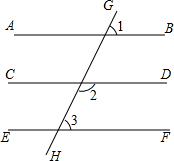 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD
如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD