题目内容
3.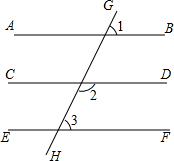 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD
如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD证明:∵∠1=70°∠3=70°
∴∠3=∠1(等量代换)
∴AB∥EF
∵∠2=110°,∠3=70° (已知)
∴∠2+∠3=180° (等式的性质)
∴CD∥EF.
∴AB∥CD(平行于同一直线的两直线平行).
分析 求出∠3=∠1,推出AB∥EF,根据平行线的判定推出CD∥EF,即可得出答案.
解答 证明:∵∠1=70°∠3=70°
∴∠3=∠1(等量代换),
∴AB∥EF,
∴∠2+∠3=180°,
∴CD∥EF,
∴AB∥CD(平行于同一直线的两直线平行),
故答案为:(等量代换),AB,EF,∠2,∠3,CD,EF,(平行于同一直线的两直线平行).
点评 本题考查了平行线的判定的应用,能正确运用平行线的判定定理进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.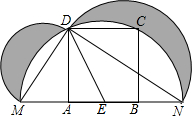 如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
 如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )| A. | 9$\sqrt{5}$ | B. | 18$\sqrt{5}$ | C. | 36$\sqrt{5}$ | D. | 72$\sqrt{5}$ |
11.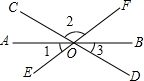 如图,直线AB、CD、EF相交于O,则∠1+∠2+∠3的度数等于( )
如图,直线AB、CD、EF相交于O,则∠1+∠2+∠3的度数等于( )
 如图,直线AB、CD、EF相交于O,则∠1+∠2+∠3的度数等于( )
如图,直线AB、CD、EF相交于O,则∠1+∠2+∠3的度数等于( )| A. | 90° | B. | 150° | C. | 180° | D. | 210° |
8.用配方法解方程x2-4x+1=0时,配方后所得的方程是( )
| A. | (x-2)2=3 | B. | (x+2)2=3 | C. | (x-2)2=1 | D. | (x-2)2=-1 |