题目内容
6．解方程组$\left\{\begin{array}{l}x+2y=4\\ 3x-2y=4\end{array}\right.$．分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{x+2y=4①}\\{3x-2y=4②}\end{array}\right.$，
①+②得：4x=8，即x=2，
把x=2代入①得：y=1，
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
17．下列方程是一元二次方程的是（ ）
| A． | 2xy-7=0 | B． | $\sqrt{2}$x2-7=0 | C． | $\frac{1}{{x}^{2}}$-7x=0 | D． | 5（x+1）=72 |
14．
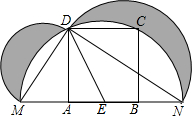如图，在边长为6的正方形ABCD中，E是AB的中点，以E为圆心，ED为半径作半圆，交A、B所在的直线于M、N两点，分别以直径MD、ND为直径作半圆，则阴影部分面积为（ ）
如图，在边长为6的正方形ABCD中，E是AB的中点，以E为圆心，ED为半径作半圆，交A、B所在的直线于M、N两点，分别以直径MD、ND为直径作半圆，则阴影部分面积为（ ）| A． | 9$\sqrt{5}$ | B． | 18$\sqrt{5}$ | C． | 36$\sqrt{5}$ | D． | 72$\sqrt{5}$ |
11．
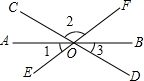如图，直线AB、CD、EF相交于O，则∠1+∠2+∠3的度数等于（ ）
如图，直线AB、CD、EF相交于O，则∠1+∠2+∠3的度数等于（ ）| A． | 90° | B． | 150° | C． | 180° | D． | 210° |