Question

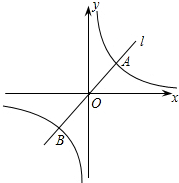
如图，P为x轴上任意一点，PB垂直于x轴，交直线y=0.5x、y=kx于A、B两点，BC⊥PB交直线y=0.5x于点C，CD⊥BC交直线y=kx于点D．解答下列问题：
（1）求线段PA与PB的比值（用k表示）；
（2）如果点D在函数y=x²图象上，求线段OP的长．

Answer 1

考点：一次函数图象上点的坐标特征,二次函数图象上点的坐标特征

专题：

分析：（1）设P点的坐标为（x，0），A、B在直线y=0.5x和y=kx上，则A点和B点的坐标分别为（x，0.5x）、（x，kx），所以PA=0.5x，PB=kx，即

PA

PB

=

0.5x

kx

=

0.5

k

．
（2）先设出P点的坐标（t，0），根据题意把B、C、D点的坐标用t表示出来，再把D点的坐标代入y=x²，即可求得OP的长度．

解答：解：（1）设P点的坐标为（x，0），
∵A、B在直线y=0.5x和y=kx上，
∴A点和B点的坐标分别为（x，0.5x）、（x，kx），．
∴PA=0.5x，PB=kx，
∴

PA

PB

=

0.5x

kx

=

0.5

k

．
（2）设P点的坐标为：（t，0）
∵PB垂直于x轴，B点在直线y=kx上，
∴B点的坐标为（t，kt），
又∵BC⊥PB交直线y=0.5x与点C，
∴C点的坐标为（2kt，kt），
又∵CD⊥BC交直线y=kx与点D，
∴D点的坐标为（2kt，2k²t）
∵D点在函数y=x²的图象上，
∴2k²t=4k²t²
解得：t=

1

2

，即OP=

1

2

．
故答案为：

0.5

k

，

1

2

．

点评：考查了函数图象上点的坐标特点，根据垂直于x轴的直线上的点，横坐标相同．垂直于y轴的直线上的点纵坐标相同，点在函数图象上，点的坐标就满足函数解析式．