题目内容
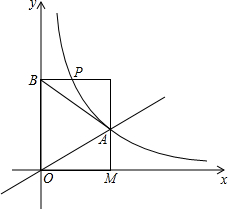 如图,在平面直角坐标系中,正比例函数y=
如图,在平面直角坐标系中,正比例函数y=| 1 |
| 2 |
| k |
| x |
(1)分别求出m和k的值;
(2)根据图象回答,当x取何值时,反比例函数的值小于正比例函数的值;
(3)若点P(x,y)在此反比例函数的图象上运动(不与点A重合),过点P作PB⊥y轴于点B,设△PAB的面积为S,求S与x的函数表达式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将A(m,2)代入y=
x,可求得m的值,得到A点坐标;再将A点坐标代入y=
,即可求出k的值;
(2)根据图象,找出反比例函数的图象落在正比例函数图象下方的部分对应的x的取值即可;
(3)由动点P(x,y)不与点A重合,得出x≠4,而x>0,所以分两种情况进行讨论:①0<x<4;②x>4.
| 1 |
| 2 |
| k |
| x |
(2)根据图象,找出反比例函数的图象落在正比例函数图象下方的部分对应的x的取值即可;
(3)由动点P(x,y)不与点A重合,得出x≠4,而x>0,所以分两种情况进行讨论:①0<x<4;②x>4.
解答:解:(1)将A(m,2)代入y=
x,
得2=
m,解得m=4;
将A(4,2)代入y=
,
得2=
,解得k=8;
(2)根据图象可得,当x>2时,反比例函数的值小于正比例函数的值;
(3)∵点P(x,y),PB⊥y轴于点B,
∴B(0,y),PB=x.
分两种情况:
①当0<x<4时,
S=
x(y-2)=
xy-x;
②当x>4时,
S=
x(2-y)=x-
xy.
| 1 |
| 2 |
得2=
| 1 |
| 2 |
将A(4,2)代入y=
| k |
| x |
得2=
| k |
| 4 |
(2)根据图象可得,当x>2时,反比例函数的值小于正比例函数的值;
(3)∵点P(x,y),PB⊥y轴于点B,
∴B(0,y),PB=x.
分两种情况:
①当0<x<4时,
S=
| 1 |
| 2 |
| 1 |
| 2 |
②当x>4时,
S=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查对一次函数与反比例函数的交点问题,用待定系数法求一次函数、反比例函数的解析式,一次函数的图象,反比例函数的图象,三角形的面积等知识点的理解和掌握,能用待定系数法求出函数的解析式和会观察图象是解此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
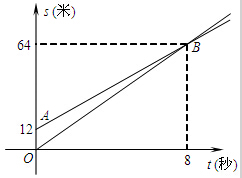 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法: 一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点.
一条铁路MN穿过公路OA.问:在铁路MN上的何处建一个货物中转站到公路OA、OB的距离相等?请在图中画出这个点. 如图:
如图: