题目内容
18. 如图所示,P是等边三角形ABC内一点,且∠APB:∠BPC:∠CPA=3:4:5,求以PA,PB,PC为边的三角形的三个内角的度数.
如图所示,P是等边三角形ABC内一点,且∠APB:∠BPC:∠CPA=3:4:5,求以PA,PB,PC为边的三角形的三个内角的度数.
分析 将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,则AP′=AP,∠P′AP=60°,得到△AP′P是等边三角形,PP′=AP,根据已知条件得到∠APB=90°,∠BPC=120°,∠CPA=150°,然后根据角的和差即可得到结论.
解答 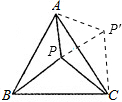 解:如图,将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,
解:如图,将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,
∵AP′=AP,∠P′AP=60°,
∴△AP′P是等边三角形,
∴PP′=AP,
∵P′C=PB,
∴△P′CP的三边长分别为PA,PB,PC,
∵∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=3:4:5,
∴∠APB=90°,∠BPC=120°,∠CPA=150°,
∴∠PP′C=∠AP′C-∠AP′P=∠APB-∠AP′P=90°-60°=30°,
∠P′PC=∠APC-∠APP′=150°-60°=90°,
∠PCP′=180°-(30°+90°)=60°,
∴以PA,PB,PC为边的三角形的三个内角的度数为:30°,60°,90°.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为10.4.
如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为10.4.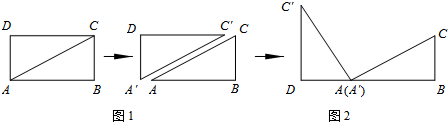
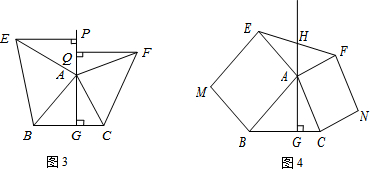
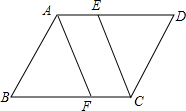 如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:
如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明: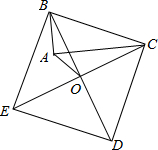 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.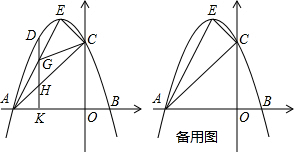
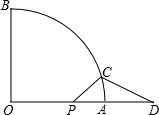 如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.
如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.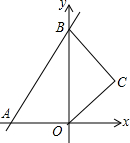 如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为$\sqrt{3}$+1.
如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为$\sqrt{3}$+1.