题目内容
18. (1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
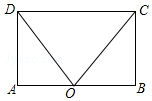
(1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.(2)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
分析 (1)把x1=3代入方程求得c的值,从而还原方程,再利用因式分解法求解可得;
(2)根据矩形的性质知∠A=∠B=90°、AD=BC,由∠AOC=∠BOD知∠AOD=∠BOC,证△AOD≌△BOC可得答案.
解答 解:(1)把x1=3代入方程得:9-12+c=0
∴c=3,
把c=3代入方程得:x2-4x+3=0
解得:x1=3,x2=1;
(2)∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵∠AOC=∠BOD,
∴∠AOC-∠DOC=∠BOD-∠DOC,
∴∠AOD=∠BOC,
在△AOD和△BOC中,
∵$\left\{\begin{array}{l}{∠A=∠B}\\{∠AOD=∠BOC}\\{AD=BC}\end{array}\right.$,
∴△AOD≌△BOC(AAS),
∴AO=OB.
点评 本题主要考查因式分解法解一元二次方程、矩形的性质、全等三角形的判定与性质,熟练掌握解一元二次方程的能力和方法及熟练掌握矩形的性质和全等三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
7.下列各数中,不是不等式2(x-5)<x-8的解的是( )
| A. | -4 | B. | -5 | C. | -3 | D. | 5 |
 如图,AC∥ED,FD∥AB,∠A=64°,求∠EDF的度数.
如图,AC∥ED,FD∥AB,∠A=64°,求∠EDF的度数. 尺规作图
尺规作图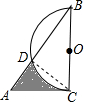 如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.
如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.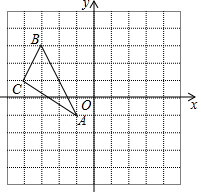 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1),画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标.
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1),画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标. 在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: