题目内容
7．
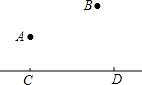如图，A，B两个小集镇在河流CD的同侧，分别到河的距离为AC=6km，BD=15km，且CD=15km，现在要在河边建一自来水厂，向A，B两镇供水，铺设水管的费用为每千米3万．试在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少．
分析 作点B关于直线CD的对称点H，连接AH交CD于M，连接BM，则MA+MB最小，根据勾股定理求出AH的长度即可．
解答 
解：作点B关于直线CD的对称点H，连接AH交CD于M，连接BM，则MA+MB最小，铺设水管的费用最节省，
作AE⊥BH于E，
∵CD=15，
∴AE=15，
EH=HD+ED=21，
∴AH=$\sqrt{A{E}^{2}+E{H}^{2}}$=26，
26×3=78万．
答：总费用是78万．
点评 本题考查的是轴对称--最短路线问题，确定铺设水管的费用最节省时点M的位置是解题的关键．
练习册系列答案
相关题目
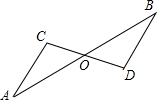如图，已知OA=OB，应填什么条件就得到△AOC≌△BOD？（允许添加一个条件）
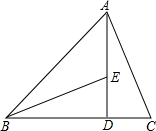如图，在△ABC中，已知AD⊥BC于点D，点E在AD上，AD=BD，DE=CD，则BE和AC有何数量关系？试用学过的知识说明．
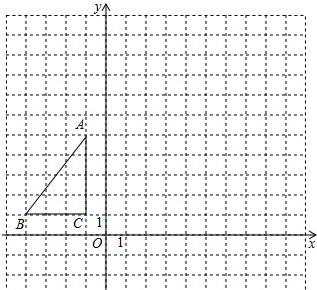如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（-1，5），B（-4，1），C（-1，1）将△ABC绕点A逆时针旋转90°，得到△AB′C′，点B，C的对应点分别为点B′，C′，