题目内容
16.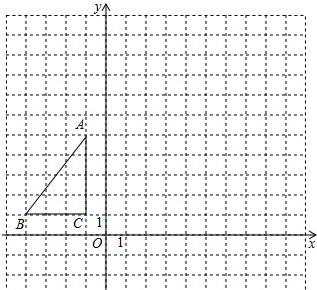 如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(-1,5),B(-4,1),C(-1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(-1,5),B(-4,1),C(-1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
分析 (1)在平面直角坐标系中画出△ABC,然后根据网格结构找出点B、C的对应点B′,C′的位置,然后顺次连接即可;
(2)根据图形即可得出点A的坐标;
(3)利用AC的长,然后根据弧长公式进行计算即可求出点B转动到点B′所经过的路程.
解答  解:(1)△AB′C′如图所示;
解:(1)△AB′C′如图所示;
(2)点B′的坐标为(3,2),点C′的坐标为(3,5);
(3)点C经过的路径为以点A为圆心,AC为半径的圆弧,路径长即为弧长,
∵AC=4,
∴弧长为:$\frac{nπr}{180°}$=$\frac{90°π•4}{180°}$=2π,
即点C经过的路径长为2π.
点评 本题考查了利用旋转变换作图,弧长的计算,熟练掌握网格结构,准确找出对应点位置作出图形是解题的关键.

练习册系列答案
相关题目
4. 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )| A. | 19° | B. | 29° | C. | 63° | D. | 73° |
11.某几何体的三视图如图所示,该几何体是( )
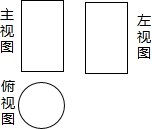

| A. | 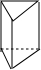 | B. |  | C. |  | D. | 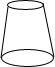 |
1.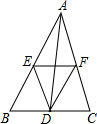 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
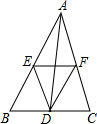 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )| A. | DE=DF | B. | EF=$\frac{1}{2}$AB | C. | S△ABD=S△ACD | D. | AD平分∠BAC |
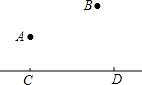 如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.
如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.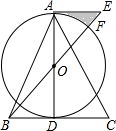 如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.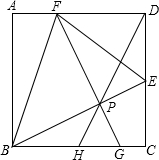 如图,点E,F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过点F作FG⊥BE于点P,交BC于点G,连接DP并延长交BC于点H,连接BF.EF.下列结论:
如图,点E,F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过点F作FG⊥BE于点P,交BC于点G,连接DP并延长交BC于点H,连接BF.EF.下列结论: