题目内容
12.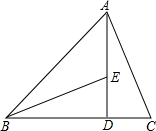 如图,在△ABC中,已知AD⊥BC于点D,点E在AD上,AD=BD,DE=CD,则BE和AC有何数量关系?试用学过的知识说明.
如图,在△ABC中,已知AD⊥BC于点D,点E在AD上,AD=BD,DE=CD,则BE和AC有何数量关系?试用学过的知识说明.
分析 根据AD⊥BC,得出∠ADC=∠BDE=90°,根据SAS证出△BDE与△ADC全等,再得出BE=AC即可.
解答 解:相等,理由如下:
∵AD⊥BC,
∴∠ADC=∠BDE=90°,
在Rt△BDE和Rt△ADC中,
$\left\{\begin{array}{l}{AD=BD}\\{∠ADC=∠BDE=90°}\\{DE=DC}\end{array}\right.$,
∴△BDE≌△ADC(SAS),
∴BE=AC.
点评 本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
3.点M(2,-1)向上平移3个单位长度得到的点的坐标是( )
| A. | (2,-4) | B. | (5,-1) | C. | (2,2) | D. | (-1,-1) |
17.实数π,$\frac{1}{5}$,$\sqrt{4}$,-1中,无理数是( )
| A. | π | B. | $\frac{1}{5}$ | C. | $\sqrt{4}$ | D. | -1 |
4. 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为( )| A. | 19° | B. | 29° | C. | 63° | D. | 73° |
1.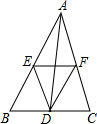 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
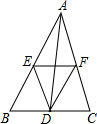 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )| A. | DE=DF | B. | EF=$\frac{1}{2}$AB | C. | S△ABD=S△ACD | D. | AD平分∠BAC |
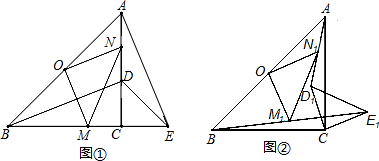
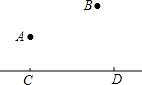 如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.
如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.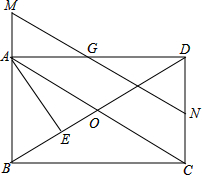 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )