题目内容
17.如图,在任意的△ABC中,分别以AB和AC为腰作等腰△ABE和等腰△ACD,AB=AE,AC=AD,且∠BAE+∠CAD=180°,连接DE,延长AC交DE于F.(1)求证:∠CAB=∠AED+∠ADE;
(2)若∠ACB=∠BAE=∠CAD=90°,如图2,求证:BC=2AF;
(3)若在△ABC中,如图3所示作等腰△ABE和等腰△ACD,AB与DE交于点F,F为DE的中点,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
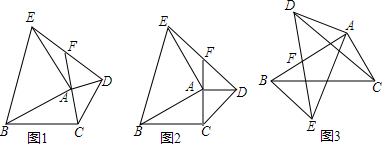
分析 (1)如图1,延长DA至G点,根据已知条件推出∠EAG+∠GAB+∠CAD=180°,由∠GAB+∠BAC+CAD=180°,于是得到∠EAB=∠CAB,根据三角形的外角的性质得到∠EAB=∠AED+∠ADE,即可得到结论;
(2)如图2,过E点作DA延长线的垂线,垂足为H,由(1)可知,∠EAH=∠BAC,推出△AHE≌△ACB,根据全等三角形的性质得到EH=BC,AH=AC,于是推出AF为△DHE中位线,根据三角形中位线的性质即可得到结论;
(3)如图,延长DA至M点,使AM=DA,连接EM,由于∠BAE+∠CAD=180°,∠CAD+∠CAM=180°,于是得到∠BAE=∠CAM推出∠BAC=CAM,证得△BAC≌△EAM,根据全等三角形的性质得到BC=EM,推出AF为△DEM中位线,根据三角形中位线的性质即可得到结论.
解答  证明:(1)如图1,延长DA至G点,
证明:(1)如图1,延长DA至G点,
∵∠BAE+∠CAD=180°,
即∠EAG+∠GAB+∠CAD=180°,
∵∠GAB+∠BAC+CAD=180°,
∴∠EAB=∠CAB,
∵∠EAB=∠AED+∠ADE,
∴∠CAB=∠AED+∠ADE,
(2)如图2,过E点作DA延长线的垂线, 垂足为H,
垂足为H,
由(1)可知,∠EAH=∠BAC,
在△AHE和△ACB中,
$\left\{\begin{array}{l}{∠AHE=∠ACB}\\{∠EAH=∠BAC}\\{AE=AB}\end{array}\right.$,
∴△AHE≌△ACB,
∴EH=BC,AH=AC,
∵AC=AD,
∴AH=AD,
∵∠EHA=∠FAD=90°,
∴AF∥EF,
∵A为DH中点,
∴AF为△DHE中位线,
∴EH=2AF,
∴BC=2AF,
(3)成立,
如图,延长DA至M点,使AM=DA,连接EM,
∵∠BAE+∠CAD=180°,
∠CAD+∠CAM=180° ,
,
∴∠BAE=∠CAM,
∴∠BAE+∠CAC=∠CAM+∠EAC,
即∠BAC=CAM,
∵AM=AD,AD=AC,
∴AM=AC,
在△BAC和△EAM中,
$\left\{\begin{array}{l}BA=EA\\∠BAC=∠EAM\\ AC=AM\end{array}\right.$,
∴△BAC≌△EAM,
∴BC=EM,
∵F、A分别为DE、DM中点,
∴AF为△DEM中位线,
∴EM=2AF,
∴BC=2AF.
点评 本题考查了全等三角形的判定和性质,三角形中位线的性质,等腰三角形的性质,三角形外角的性质,正确的作出辅助线是解题的关键.


| A. | ①②⑥ | B. | ①③⑤ | C. | ②③⑤ | D. | ②③④ |
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
| A. | -22014 | B. | 22014 | C. | 1 | D. | -22015 |
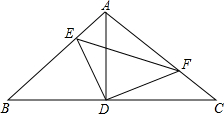 如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )
如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )| A. | △ADF≌△BDE | B. | S四边形AEDF=$\frac{1}{2}$S△ABC | ||
| C. | BE+CF=$\sqrt{2}$AD | D. | EF=AD |
 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
| A. | +7 | B. | -2.3 | C. | 0.53 | D. | 0 |
