题目内容
2.如图1,四边形OABC中,OA=a,OC=8,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).(1)若点D与点A重合,则θ=45°,a=8;
(2)若折叠后点D恰为AB的中点(如图2),求θ的度数.

分析 (1)利用轴对称的性质即可解决问题;
(2)延长MD、OA,交于点N,如图2.易证△BDM≌△ADN,则有DM=DN,根据垂直平分线的性质可得OM=ON,根据等腰三角形的性质可得∠MOD=∠NOD,从而就可求出θ.
解答 解:(1)若点D与点A重合,
则θ=$\frac{1}{2}$∠COA=45°,OA=OC=8.
故答案为:45°,8.
(2)如图:延长MD、OA,交于点N.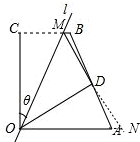
∵∠AOC=∠BCO=90°,
∴∠AOC+∠BCO=180°,
∴BC∥OA,
∴∠B=∠DAN.
在△BDM和△ADN中,
$\left\{\begin{array}{l}{∠B=∠DAN}\\{BD=AD}\\{∠BDM=∠ADN}\end{array}\right.$,
∴△BDM≌△ADN(ASA),
∴DM=DN.
∵∠ODM=∠OCM=90°,
∴根据线段垂直平分线的性质可得OM=ON,
∴根据等腰三角形的性质可得∠MOD=∠NOD.
由折叠可得∠MOD=∠MOC=θ,
∴∠COA=3θ=90°,
∴θ=30°.
点评 本题主要考查了轴对称的性质、线段垂直平分线的性质、等腰三角形的性质、全等三角形的性质和判定,构造全等三角形是解决第(2)小题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列运用平方差公式进行计算,错误的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | (x+1)(x-1)=x2-1 | ||
| C. | (-3x+2)(-3x-2)=9x2-4 | D. | (2x+1)(2x-1)=2x2-1 |
11.抛物线y=x2+2的图象与y轴的交点坐标是( )
| A. | (-2,0) | B. | (2,0) | C. | (0,-2) | D. | (0,2) |
12.|-13|=( )
| A. | -9 | B. | -13 | C. | 13 | D. | 9 |
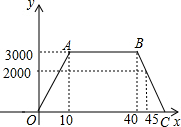 (1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求:
(1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求:
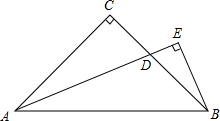 已知,如图在△ABC中,AC=BC,∠C=90°,AD平分∠BAC,BE⊥AE于E.
已知,如图在△ABC中,AC=BC,∠C=90°,AD平分∠BAC,BE⊥AE于E.