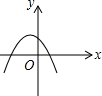题目内容
9.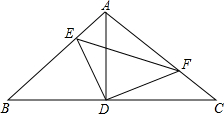 如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )
如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )| A. | △ADF≌△BDE | B. | S四边形AEDF=$\frac{1}{2}$S△ABC | ||
| C. | BE+CF=$\sqrt{2}$AD | D. | EF=AD |
分析 根据等腰直角三角形的性质得到AD=BD=CD,∠ADB=∠ADC=90°,∠B=∠C=∠BAD=∠CAD=45°,根据余角的性质得到∠BDE=∠ADF,于是得到△ADF≌△BDE,证得S△ADF=S△BDE,推出S四边形AEDF=S△ADE+S△ADF=S△ADE+S△BDE-S△ABD,得到S四边形AEDF=$\frac{1}{2}$S△ABC,根据全等三角形的性质得到AF=BE,等量代换得到BE+CF=AF+CF=AC=$\sqrt{2}$AD,由等腰直角三角形的性质得到AD=$\frac{1}{2}$BC,当EF∥BC时,EF=$\frac{1}{2}$BC,而EF不一定平行于BC,即可得到结论.
解答 解:∵∠BAC=90°,AB=AC,点D为BC的中点,
∴AD=BD=CD,∠ADB=∠ADC=90°,∠B=∠C=∠BAD=∠CAD=45°,
∵∠EDF=90°,
∴∠BDE+∠ADE=∠ADE+∠ADF=90°,
∴∠BDE=∠ADF,
在△ADF与△BDE中,$\left\{\begin{array}{l}{∠B=∠DAF}\\{AD=BD}\\{∠ADF=∠BDE}\end{array}\right.$,
∴△ADF≌△BDE,
∴S△ADF=S△BDE,
∵S四边形AEDF=S△ADE+S△ADF=S△ADE+S△BDE-S△ABD,
∵S△ABD=$\frac{1}{2}$S△ABC,
∴S四边形AEDF=$\frac{1}{2}$S△ABC,
∵△ADF≌△BDE,
∴AF=BE,
∴BE+CF=AF+CF=AC=$\sqrt{2}$AD,
∵AD=$\frac{1}{2}$BC,
当EF∥BC时,EF=$\frac{1}{2}$BC,
而EF不一定平行于BC,
∴EF不一定等于$\frac{1}{2}$BC,
∴EF≠AD,
故选D.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形面积的计算,熟练掌握全等三角形的判定和性质是解题的关键.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | -(-2)3 | B. | -24 | C. | (-1)×(-3)5 | D. | 23×(-2)6 |
| A. | t>8 | B. | t≤26 | C. | 8<t<26 | D. | 8≤t≤26 |
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
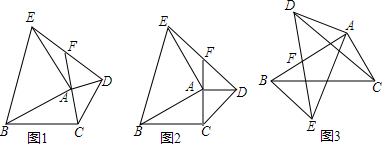
 如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形中小箭头的方向是向上(填写:上、下、左、右).
如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形中小箭头的方向是向上(填写:上、下、左、右).
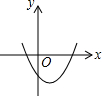
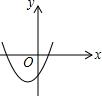
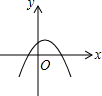
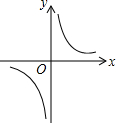 已知反比例函数y=$\frac{ab}{x}$(ab≠0)的图象如图所示,则二次函数y=ax2+bx-2的大致图象是( )
已知反比例函数y=$\frac{ab}{x}$(ab≠0)的图象如图所示,则二次函数y=ax2+bx-2的大致图象是( )