题目内容
9. 如图,在△ABC中,∠ABC=45°,AC=8,AD⊥BC于D,BE⊥AC于E,AD、BE相交于点F,求线段BF的长.
如图,在△ABC中,∠ABC=45°,AC=8,AD⊥BC于D,BE⊥AC于E,AD、BE相交于点F,求线段BF的长.
分析 利用条件可证明△BDF≌△ADC,则可得到BF=AC,可求得BF的长.
解答 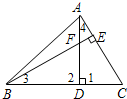 解:
解:
∵AD⊥BC于D,且∠ABC=45°,
∴∠BAD=90°-∠ABC=45°,
∴AD=BD,
又∵AD⊥BC,BE⊥AC,
∴∠1=∠2=90°,
∴∠3=90°-∠BFD,
∠4=90°-∠AFE,
又∵∠AFE=∠BFD,
∴∠3=∠4,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠3=∠4}\\{AD=BD}\\{∠1=∠2}\end{array}\right.$
∴△BDF≌△ADC(ASA),
∴BF=AC,
又∵AC=8,
∴BF=8.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定和性质是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
17.某校从八年级(一)班和(二)班各选取了10名女学生,其身高如下:(单位:厘米)
(一)班:168 167 170 165 168 166 171 168 167 170
(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表
(2)本校打算从八年级(一)班和(二)班中只选一个班的10名女生组成礼仪队.要求身高较整齐,你认为哪个班较为合适,为什么?
(一)班:168 167 170 165 168 166 171 168 167 170
(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表
| 班级 | 平均分 | 方差 | 中位数 | 极差 |
| 一班 | 168 | 168 | 6 | |
| 二班 | 168 | 3.8 |
4.如表是某校八年级(1)班20名学生某次数学测验的成绩统计表.
若这20名学生成绩的平均分数为82分,求x和y的值.
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 5 | x | y | 2 |
 如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.若△BED的面积为28,△DFC的面积为21,求△DEF的面积.
如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.若△BED的面积为28,△DFC的面积为21,求△DEF的面积.