题目内容
13.已知二次函数y=mx2-3mx-4m(m≠0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C且∠ACB=90°,则m的值为( )| A. | ±2 | B. | ±4 | C. | ±$\frac{1}{2}$ | D. | ±$\frac{1}{4}$ |
分析 首先求出点A、B、C的坐标,由已知条件易证△AOC∽△COB,再根据相似三角形的性质即可求出m的值.
解答 解:
设y=0,则=mx2-3mx-4m=0,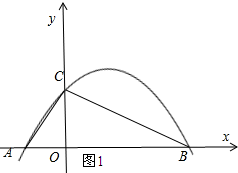
解得:m=4或m=-1,
∵点A在点B的左侧,
∴OA=1,OB=4,
设x=0,则y=-4m,
∴OC=|-4m|,
∵∠ACO+∠OCB=90°,∠CAO+∠ACO=90°,
∴∠CAO=∠BCO,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴$\frac{AO}{OC}=\frac{OC}{OB}$,
∴OC2=OA•OB,
即16m2=4,
解得:m=±$\frac{1}{4}$,
故选D.
点评 本题考查了抛物线和坐标轴交点的问题、相似三角形的判断和性质,能够证明△AOC∽△COB是解题的关键.

练习册系列答案
相关题目
3. 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )| A. | 汽车共行驶了120千米 | |
| B. | 汽车在整个行驶过程中平均速度为40千米 | |
| C. | 汽车返回时的速度为80千米/时 | |
| D. | 汽车自出发后1.5小时至2小时之间速度不变 |
4.一个三角形的两边长分别为3和7,第三边长为整数,则第三边长度的最小值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.数轴上的点A在原点的左侧,且到原点的距离是2,则点A表示的数为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
 画出如图所示几何体的主视图、左视图和俯视图,其中正确的是( )
画出如图所示几何体的主视图、左视图和俯视图,其中正确的是( )



 如图,?ABCD的顶点O,A,C的坐标分别是(0,0),(-5,0),(-2,3),则顶点B的坐标是(-7,3).
如图,?ABCD的顶点O,A,C的坐标分别是(0,0),(-5,0),(-2,3),则顶点B的坐标是(-7,3).



 如图,已知△ABC中,∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是多少?
如图,已知△ABC中,∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是多少?