题目内容
已知正比例函数y1=k1x(k1≠0)和反比例函数y2=
(k2≠0),x与y1和y2的部分应对值如下表所示:
(1)求m,n,p的值;
(2)指出正比例函数图象与反比例函数图象的交点坐标;
(3)设A(4,n),B(8,p),点G在x轴上,且GA=GB.求点G的坐标.
| k2 |
| x |
(1)求m,n,p的值;
(2)指出正比例函数图象与反比例函数图象的交点坐标;
(3)设A(4,n),B(8,p),点G在x轴上,且GA=GB.求点G的坐标.
| x | … | m | 4 | 8 | … | ||
| y1=k1x | … | 1 | n | 4 | … | ||
y2=
| … | 4 | 2 | p | … |
考点:反比例函数综合题
专题:计算题
分析:(1)把(8,4)代入正比例解析式求出k1的值,确定出正比例解析式,即可求出m与n的值;把(4,2)代入反比例解析式求出k2的值,确定出反比例解析式,即可求出p的值;
(2)联立正比例与反比例解析式,求出交点坐标即可;
(3)由n与p的值确定出A与B的坐标,设G(x,0),根据GA=GB,利用两点间的距离公式列出方程,求出方程的解得到x的值,即可确定出G坐标.
(2)联立正比例与反比例解析式,求出交点坐标即可;
(3)由n与p的值确定出A与B的坐标,设G(x,0),根据GA=GB,利用两点间的距离公式列出方程,求出方程的解得到x的值,即可确定出G坐标.
解答:解:(1)把(8,4)代入y1=k1x中,得:k1=
,即y1=
x,
把y1=1代入得:m=2,把x=4,代入得:n=2;
把(4,2)代入y2=
中,得:k2=8,即y2=
,
把x=8代入得:p=1;
(2)联立得:
,
解得:
或
,
则正比例函数与反比例函数图象的交点坐标为(4,2)或(-4,-2);
(3)根据题意得:A(4,2),B(8,1),设G(x,0),
由GA=GB,得到
=
,
解得:x=
,
则G(
,0).
| 1 |
| 2 |
| 1 |
| 2 |
把y1=1代入得:m=2,把x=4,代入得:n=2;
把(4,2)代入y2=
| k2 |
| x |
| 8 |
| x |
把x=8代入得:p=1;
(2)联立得:
|
解得:
|
|
则正比例函数与反比例函数图象的交点坐标为(4,2)或(-4,-2);
(3)根据题意得:A(4,2),B(8,1),设G(x,0),
由GA=GB,得到
| (x-4)2+22 |
| (x-8)2+12 |
解得:x=
| 35 |
| 8 |
则G(
| 35 |
| 8 |
点评:此题属于反比例综合题,涉及的知识有:待定系数法确定正比例及反比例解析式,正比例函数与反比例函数的交点,以及两点间的距离公式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
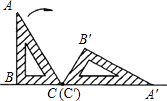 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置.若AC=15cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置.若AC=15cm,那么顶点A从开始到结束所经过的路径长为( )| A、10πcm | ||
B、10
| ||
| C、15πcm | ||
| D、20πcm |
 如图,四边形ABCD中,∠A=60°,∠B=∠D=90°,AB=4,CD=2,求BC和AD的长.
如图,四边形ABCD中,∠A=60°,∠B=∠D=90°,AB=4,CD=2,求BC和AD的长. 如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为
如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为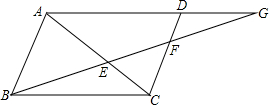 如图,在平行四边形ABCD中,BE=3,EF=2,求:
如图,在平行四边形ABCD中,BE=3,EF=2,求: