题目内容
10.某工厂要加工一批零件,若甲车间单独做需要40天完成,乙车间单独做需要60天完成,现安排甲车间先做十天,然后甲乙两车间共同做.设甲车间一共做了x天,则根据题意列出的方程为$\frac{1}{40}$x+$\frac{1}{60}$(x-10)=1.分析 合作的天数减10即可确定乙工作的天数,利用总的工作量为1列出方程即可.
解答 解:若甲先干一天,然后,甲、乙合作完成此项工作,若设甲一共做了x天,乙工作的天数为(x-10),
根据题意得:$\frac{1}{40}$x+$\frac{1}{60}$(x-10)=1,
故答案为:$\frac{1}{40}$x+$\frac{1}{60}$(x-10)=1
点评 本题考查了由实际问题抽象出一元一次方程,找到关键描述语,找到等量关系是解决问题的关键.工程问题中常用的关系式有:工作时间=工作总量÷工作效率.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列各组单项式中,是同类项的是( )
| A. | 5x2y与-3xy2 | B. | 8xy2与-2x2z | C. | 10abc与-8ab | D. | 5ab与-5ba |
15.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=22℃时,某人看到烟花燃放5秒后才听到响声,那么此人与烟花燃放处的距离多远?
| 气温x(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
②求出y与x之间的表达式;
③气温x=22℃时,某人看到烟花燃放5秒后才听到响声,那么此人与烟花燃放处的距离多远?
2. 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
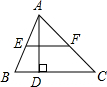 如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.
如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.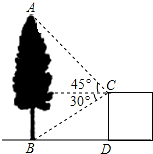 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,求大树的高度.
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,求大树的高度.