题目内容
12.思考探究思考.
(1)计算:$\sqrt{{2}^{2}}$=2;$\sqrt{(-\frac{2}{3})^{2}}$=$\frac{2}{3}$;$\sqrt{{0}^{2}}$=0.
(2)计算:($\sqrt{2}$)2=2;($\sqrt{\frac{2}{3}}$)2=$\frac{2}{3}$;($\sqrt{0}$)2=0.
探究
(3)对于任意实数a,$\sqrt{{a}^{2}}$=|a|.
(4)对于任意非负实数a,($\sqrt{a}$)2=a.
分析 (1)直接利用算术平方根的性质化简求出答案;
(2)直接利用二次根式的性质化简求出答案;
(3)结合(1)中所求进而得出一般规律;
(4)结合(2)中所求得出一般规律.
解答 解:(1)$\sqrt{{2}^{2}}$=2;$\sqrt{(-\frac{2}{3})^{2}}$=$\frac{2}{3}$;$\sqrt{{0}^{2}}$=0.
故答案为:2,$\frac{2}{3}$,0;
(2)($\sqrt{2}$)2=2;($\sqrt{\frac{2}{3}}$)2=$\frac{2}{3}$;($\sqrt{0}$)2=0.
故答案为:2,$\frac{2}{3}$,0;
(3)对于任意实数a,$\sqrt{{a}^{2}}$=|a|.
故答案为:|a|;
(4)对于任意非负实数a,($\sqrt{a}$)2=a.
故答案为:a.
点评 此题主要考查了算式平方根的性质,正确得出一般规律是解题关键.

练习册系列答案
相关题目
3.如果代数式a-6比2a-3的值少1,那么代数式3a+1的值是( )
| A. | -5 | B. | 5 | C. | 7 | D. | -7 |
20. 如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )
如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )
 如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )
如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )| A. | 58° | B. | 32° | C. | 80° | D. | 64° |
5.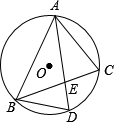 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则AE的长为( )
如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则AE的长为( )
 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则AE的长为( )
如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则AE的长为( )| A. | $\frac{4}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{32}{25}$ | D. | $\frac{21}{5}$ |
9. 如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
 如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )| A. | 65° | B. | 70° | C. | 75° | D. | 80° |
 两个相同的矩形ABCD和AEFG如图摆放,点E在AD上,AB=1,BC=2,连结GC,交EF于点H,连结HB,那么HB的长是$\frac{\sqrt{13}}{2}$.
两个相同的矩形ABCD和AEFG如图摆放,点E在AD上,AB=1,BC=2,连结GC,交EF于点H,连结HB,那么HB的长是$\frac{\sqrt{13}}{2}$.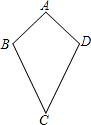 【问题提出】
【问题提出】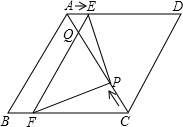 如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).
如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).