题目内容
1.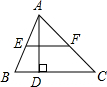 如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.
如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.
分析 过O作OP⊥BC,交BC于点P,由E、F分别为AB、AC的中点,即EF为三角形ABC的中位线,利用中位线定理得到EF=$\frac{1}{2}$BC,且EF∥BC,由AD=$\frac{1}{2}$BC,等量代换得到EF=AD,由平行线等分线段性质得到OP=$\frac{1}{2}$AD,即OP=$\frac{1}{2}$EF,由EF为圆O的直径,得到OP为圆的半径,即可得到BC与圆O相切.
解答 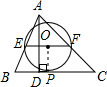 解:圆O与BC相切,
解:圆O与BC相切,
理由:过O作OP⊥BC,交BC于点P,如图所示:
∵EF为△ABC的中位线,
∴E、F分别为AB、AC的中点,
∴EF=$\frac{1}{2}$BC,EF∥BC,
∵AD=$\frac{1}{2}$BC,
∴EF=AD,
∴OP=$\frac{1}{2}$AD=$\frac{1}{2}$EF,
∵EF为圆O的直径,
∴OP为圆的半径,
∴BC为圆O的切线,即圆O与BC相切.
点评 此题考查的是直线与圆的位置关系,根据题意画出图形,利用数形结合求解是解答本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
3.如果代数式a-6比2a-3的值少1,那么代数式3a+1的值是( )
| A. | -5 | B. | 5 | C. | 7 | D. | -7 |
9. 如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
 如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )| A. | 65° | B. | 70° | C. | 75° | D. | 80° |
11.下列图形:角、线段、等边三角形、钝角三角形、平行四边形,其中轴对称图形有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
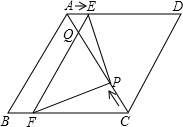 如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).
如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).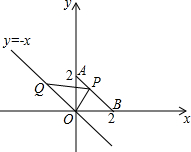 如图,在平面直角坐标系中,点A的坐标是(0,2),点B的坐标是(2,0),连结AB,点P是线段AB上的一个动点(包括两端点),直线y=-x上有一动点Q,连结OP,PQ,已知△OPQ的面积为$\sqrt{2}$,则点Q的坐标为($\sqrt{2}$,-$\sqrt{2}$)或(-$\sqrt{2}$,$\sqrt{2}$)..
如图,在平面直角坐标系中,点A的坐标是(0,2),点B的坐标是(2,0),连结AB,点P是线段AB上的一个动点(包括两端点),直线y=-x上有一动点Q,连结OP,PQ,已知△OPQ的面积为$\sqrt{2}$,则点Q的坐标为($\sqrt{2}$,-$\sqrt{2}$)或(-$\sqrt{2}$,$\sqrt{2}$)..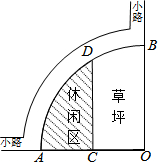 如图是某公园的一角,∠AOB=90°,弧AB半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,求图中休闲区(阴影部分)的面积.
如图是某公园的一角,∠AOB=90°,弧AB半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,求图中休闲区(阴影部分)的面积.