题目内容
18.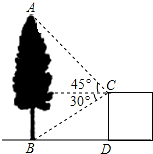 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,求大树的高度.
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,求大树的高度.
分析 根据正切的定义求出EC,根据等腰直角三角形的性质求出AE,计算即可.
解答  解:如图,由题意得,BE=CD=5m,
解:如图,由题意得,BE=CD=5m,
在Rt△CBE中,EC=$\frac{BE}{tan∠BCE}$=5$\sqrt{3}$米,
∵∠ECA=45°,
∴AE=EC=5$\sqrt{3}$米,
∴大树的高为(5$\sqrt{3}$+5)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,理解仰角俯角的概念、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
20. 如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )
如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )
 如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )
如图,AB是⊙O的直径,弦CD与AB相交,且∠ABC=32°,则∠CDB的度数为( )| A. | 58° | B. | 32° | C. | 80° | D. | 64° |
9. 如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
 如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )
如图,点D在BC的延长线上,∠A=35°,∠B=40°,则∠1的度数为( )| A. | 65° | B. | 70° | C. | 75° | D. | 80° |
3.下列变量间的关系不是函数关系的是( )
| A. | 长方形的宽一定,其长与面积 | B. | 正方形的周长与面积 | ||
| C. | 圆柱的底面半径与体积 | D. | 圆的周长与半径 |
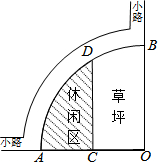 如图是某公园的一角,∠AOB=90°,弧AB半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,求图中休闲区(阴影部分)的面积.
如图是某公园的一角,∠AOB=90°,弧AB半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,求图中休闲区(阴影部分)的面积. 如图,将边长为6的等边△ABC放置在平面直角坐标系中,则A点坐标为(3,3$\sqrt{3}$).
如图,将边长为6的等边△ABC放置在平面直角坐标系中,则A点坐标为(3,3$\sqrt{3}$).