题目内容
14.先化简,再求值:$\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{4x}{x-1}$,x=-1.分析 根据分式的减法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:$\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{4x}{x-1}$
=$\frac{2{x}^{2}+2x-4x(x+1)}{(x+1)(x-1)}$
=$\frac{2{x}^{2}+2x-4{x}^{2}-4x}{(x+1)(x-1)}$
=$\frac{-2{x}^{2}-2x}{(x+1)(x-1)}$
=$\frac{-2x(x+1)}{(x+1)(x-1)}$
=$-\frac{2x}{x-1}$,
当x=-1时,原式=$-\frac{2×(-1)}{-1-1}$=-1.
点评 本题考查分式的化简求值,解答此类问题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:BC=ED.
如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:BC=ED. 如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3=12.
如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为S1,S2,S3,且S1=4,S2=8,则S3=12.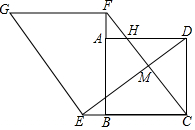 如图,在正方形ABCD中,点E,F分别是CB,BA延长线上的点,且BE=AF,连接DE,CF,CF交DE于点M,交AD于点H,过点E作EG⊥DE,使EG=DE,连接FG.
如图,在正方形ABCD中,点E,F分别是CB,BA延长线上的点,且BE=AF,连接DE,CF,CF交DE于点M,交AD于点H,过点E作EG⊥DE,使EG=DE,连接FG. 如图,已知点A,B,C在同一平面内,按要求完成下列各小题.
如图,已知点A,B,C在同一平面内,按要求完成下列各小题. 已知Rt△ABC中∠C=90°,AC=3,BC=4,以三角形一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )个.
已知Rt△ABC中∠C=90°,AC=3,BC=4,以三角形一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )个.